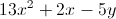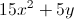All HSPT Math Resources
Example Questions
Example Question #571 : Problem Solving
Simplify the expression:
2x
x2 + 2x + 1
2x + 1
x + 1
x
x + 1
Factor out a (2x) from the denominator, which cancels with (2x) from the numerator. Then factor the numerator, which becomes (x + 1)(x + 1), of which one of them cancels and you're left with (x + 1).
Example Question #71 : Simplifying Expressions
Simplify the following expression: x3 - 4(x2 + 3) + 15
To simplify this expression, you must combine like terms. You should first use the distributive property and multiply -4 by x2 and -4 by 3.
x3 - 4x2 -12 + 15
You can then add -12 and 15, which equals 3.
You now have x3 - 4x2 + 3 and are finished. Just a reminder that x3 and 4x2 are not like terms as the x’s have different exponents.
Example Question #571 : Problem Solving
Simplify the following expression:
2x(x2 + 4ax – 3a2) – 4a2(4x + 3a)
–12a3 – 14ax2 + 2x3
12a3 – 22a2x + 8ax2 + 2x3
–12a3 – 14a2x + 2x3
–12a3 – 22a2x + 8ax2 + 2x3
12a3 – 16a2x + 8ax2 + 2x3
–12a3 – 22a2x + 8ax2 + 2x3
Begin by distributing each part:
2x(x2 + 4ax – 3a2) = 2x * x2 + 2x * 4ax – 2x * 3a2 = 2x3 + 8ax2 – 6a2x
The second:
–4a2(4x + 3a) = –16a2x – 12a3
Now, combine these:
2x3 + 8ax2 – 6a2x – 16a2x – 12a3
The only common terms are those with a2x; therefore, this reduces to
2x3 + 8ax2 – 22a2x – 12a3
This is the same as the given answer:
–12a3 – 22a2x + 8ax2 + 2x3
Example Question #572 : Problem Solving
Which of the following does not simplify to 
All of these simplify to
5x – (6x – 2x) = 5x – (4x) = x
(x – 1)(x + 2) - x2 + 2 = x2 + x – 2 – x2 + 2 = x
x(4x)/(4x) = x
(3 – 3)x = 0x = 0
Example Question #2 : How To Simplify Expressions
Simplify:
In order to simplify this expression, distribute and multiply the outer term with the two inner terms.
Example Question #3 : How To Simplify Expressions
Simplify:
When the same bases are multiplied, their exponents can be added. Similarly, when the bases are divided, their exponents can be subtracted. Apply this rule for the given problem.
Example Question #4 : How To Simplify Expressions
Simplify:
To simplify this expression, reduce the term inside the parenthesis.
Rewrite the negative exponent as a fraction.
Example Question #11 : How To Simplify Expressions
Simplify the expression
To simplify this expression, combine like terms. In this expression, 





Therefore, the correct answer is
Example Question #12 : How To Simplify Expressions
Simplify the expression
To simplify this expression, combine like terms. In this expression, 





Therefore, the correct answer is
Example Question #11 : How To Simplify Expressions
Simplify the expression:
Combine all the like terms.
The 

When you combine the 

There is only one 

Certified Tutor
Certified Tutor
All HSPT Math Resources