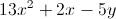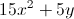Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : Algebra

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #91 : Algebra

Solve:

$18\div(5-2)$

Possible Answers:

Correct answer:

Explanation:

$18\div(5-2)$

When solving this problem, remember order of operations PEMDAS. The parentheses come first followed by the division.

5-2=3

$18\div3=6$

Report an Error

Example Question #85 : Common Core Math: Grade 5

Solve:

$16+3\times9+(42-10)$

Possible Answers:

Correct answer:

Explanation:

$16+3\times9+(42-10)$

When solving this problem, remember order of operations PEMDAS. The parentheses come first, followed by the multiplication, and then addition.

42-10=32

$3\times9=27$

16+27+32=75

Report an Error

Example Question #1 : Word Problems

Mark is three times as old as his son Brian. In ten years, Mark will be years old. In how many years will Mark be twice as old as Brian?

Possible Answers:

Correct answer:

Explanation:

In ten years, Mark will be years old, so Mark is 43-10 = 33 years old now, and Brian is one-third of this, or $33 \div 3 = 11$ years old.

Let be the number of years in which Mark will be twice Brian's age. Then Brian will be N + 11 , and Mark will be N + 33 . Since Mark will be twice Brian's age, we can set up and solve the equation:

2 (N + 11) = N + 33

2N + 22 = N + 33

2N + 22-N - 22 = N + 33 -N - 22

N = 11

Mark will be twice Brian's age in years.

Report an Error

Example Question #2 : Solve Word Problems Leading To Equations: Ccss.Math.Content.7.Ee.B.4a

Gary is twice as old as his niece Candy. How old will Candy will be in five years when Gary is years old?

Possible Answers:

Not enough information is given to determine the answer.

Correct answer:

Explanation:

Since Gary will be 37 in five years, he is 37 - 5 = 32 years old now. He is twice as old as Cathy, so she is $32 \div 2 =16$ years old, and in five years, she will be 16 + 5 = 21 years old.

Report an Error

Example Question #34 : Solve Word Problems Leading To Inequalities: Ccss.Math.Content.7.Ee.B.4b

A parking garage charges a minimum fee of $\$7$ to park in the garage. It also charges an additional fee of $\$2$ for every hour, or portion of an hour, in which a person parks in the garage. Cliff wants to pay a maximum of $\$20$ to park there. If he pulls into the garage at exactly $7\textup{:}00\textup { AM}$ , when must he leave at latest?

Possible Answers:

$2\textup{:}30\textup { PM}$

$1\textup{:}00\textup { PM}$

$1\textup{:}30\textup { PM}$

$12\textup{:}30\textup { PM}$

Correct answer:

$1\textup{:}00\textup { PM}$

Explanation:

Let be the number of hours that Cliff parks his car in the garage. Since he pays a flat fee of $\$7$ plus $\$2$ per hour or portion thereof, he pays 2X + 7 dollars. Since he does not want to spend more than $\$20$ ,

$2X + 7 \leq 20$

$2X + 7 - 7 \leq 20 - 7$

$2X \leq 13$

$2X \div 2 \leq 13 \div 2$

$X \leq 6.5$

Since a portion of an hour counts as much as an hour, must be a whole number.

$X \leq 6.5$

implies that

$X \leq 6$ .

Cliff can park in the garage for a maximum of 6 hours, and since he entered the garage at $7:00\textup { AM}$ , he must exit hours later:

7+ 6 - 12 = 1 ,

or $1:00\textup { PM}$ .

Report an Error

Example Question #82 : How To Solve Two Step Equations

Solve the following:

$(12+13)\times2$

Possible Answers:

Correct answer:

Explanation:

$(12+13)\times2$

When solving this problem, remember order of operations PEMDAS. The parentheses come first followed by the multiplication.

12+13=25

$25\times2=50$

Report an Error

Example Question #1145 : Isee Middle Level (Grades 7 8) Quantitative Reasoning

Solve:

$(34+17)\times2$

Possible Answers:

102

Correct answer:

102

Explanation:

$(34+17)\times2$

When solving this problem, remember order of operations PEMDAS. The parentheses come first followed by the multiplication.

34+17=51

$51\times2=102$

Report an Error

Example Question #1 : How To Simplify Expressions

You are given that A,B,C are whole numbers.

Which of the following is true of AB +C if and are both odd?

Possible Answers:

AB +C is always even.

AB +C is always odd if is even, and always even if is odd.

AB +C is always odd.

None of the other statements are true.

AB +C is always odd if is odd, and always even if is even.

Correct answer:

AB +C is always odd if is even, and always even if is odd.

Explanation:

If is odd, then is odd, since the product of two odd whole numbers must be odd. When the odd number is added, the result, AB +C , is even, since the sum of two odd numbers must be even.

If is even, then is even, since the product of an odd number and an even number must be even. When the odd number is added, the result, AB +C , is odd, since the sum of an odd number and an even number must be odd.

Report an Error

Example Question #2 : How To Simplify Expressions

Simplify the expression:

3x^2+9x+10x^2+5y+(-11x)

Possible Answers:

11x^2+5y

13x^2+2x-5y

13x^2-2x+5y

15x^2+5y

Correct answer:

13x^2-2x+5y

Explanation:

Combine all the like terms.

The x^2 terms can be combined together, which gives you 13x^2 .

When you combine the terms together, you get -2x .

There is only one term so it doesn't get combined with anything. Put them all together and you get

13x^2-2x+5y .

Report an Error

Example Question #3 : How To Simplify Expressions

Simplify the following expression:

$\dpi{100} \small 2(4x-3x)-6t+5x$

Possible Answers:

$\dpi{100} \small 7x-6t$

$\dpi{100} \small 1x-6t+5$

$\dpi{100} \small 6t-7x$

$\dpi{100} \small 6x+11x$

$\dpi{100} \small 14x - 11xt$

Correct answer:

$\dpi{100} \small 7x-6t$

Explanation:

$\dpi{100} \small 2(4x-3x)-6t+5x$

First distribute the 2: $\dpi{100} \small 8x-6x-6t+5x$

Combine the like terms: $\dpi{100} \small 7x-6t$

Report an Error

View Tutors

Samarth
Certified Tutor

Maharaja Sayajirao University of Baroda, Bachelor of Engineering, Mechanical Engineering. Concordia University-Seward, Master...

View Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

View Tutors

Ana Maria
Certified Tutor

Florida International University, Bachelor of Science, Mathematics Teacher Education.

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Boston, MCAT Tutors in Miami, Statistics Tutors in San Diego, SSAT Tutors in Philadelphia, French Tutors in New York City, Statistics Tutors in Atlanta, Physics Tutors in Seattle, LSAT Tutors in Miami, ACT Tutors in Washington DC, Reading Tutors in San Francisco-Bay Area

Popular Courses & Classes

MCAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Chicago, GMAT Courses & Classes in Philadelphia, GRE Courses & Classes in Phoenix, SSAT Courses & Classes in Denver, MCAT Courses & Classes in San Diego, ISEE Courses & Classes in Boston, SAT Courses & Classes in Washington DC, Spanish Courses & Classes in Philadelphia, MCAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

MCAT Test Prep in Los Angeles, LSAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Washington DC, GMAT Test Prep in Denver, SAT Test Prep in New York City, ISEE Test Prep in Phoenix, GMAT Test Prep in Chicago, GMAT Test Prep in Philadelphia, MCAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : Algebra

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #91 : Algebra

Example Question #85 : Common Core Math: Grade 5

Example Question #1 : Word Problems

Example Question #2 : Solve Word Problems Leading To Equations: Ccss.Math.Content.7.Ee.B.4a

Example Question #34 : Solve Word Problems Leading To Inequalities: Ccss.Math.Content.7.Ee.B.4b

Example Question #82 : How To Solve Two Step Equations

Example Question #1145 : Isee Middle Level (Grades 7 8) Quantitative Reasoning

Example Question #1 : How To Simplify Expressions

Example Question #2 : How To Simplify Expressions

Example Question #3 : How To Simplify Expressions

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: