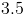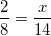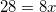All High School Math Resources
Example Questions
Example Question #2 : Quadrilaterals
When polygons are similar, the sides will have the same ratio to one another. Set up the appropriate proportions.
Cross multiply.
Example Question #1 : Quadrilaterals
Find the area of the following trapezoid:

The formula for the area of a trapezoid is:
Where 


To find the height of the trapezoid, use a Pythagorean triple:
Plugging in our values, we get:
Example Question #7 : Quadrilaterals
Find the area of the following trapezoid:

Use the formula for 
The formula is:
Where 

Beginning with the 



Creating another 



The formula for the area of a trapezoid is:
Where 


Plugging in our values, we get:
Example Question #8 : Quadrilaterals
Determine the area of the following trapezoid:

The formula for the area of a trapezoid is:

where 


Plugging in our values, we get:
Example Question #1 : Trapezoids
Find the area of the following trapezoid:

The formula for the area of a trapezoid is:

where 


Use the Pythagorean Theorem to find the height of the trapezoid:
Plugging in our values, we get:
Example Question #1 : Trapezoids
Find the area of the following trapezoid:
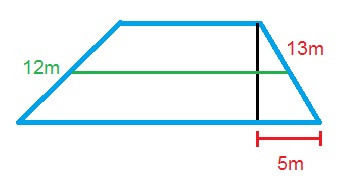
The formula for the area of a trapezoid is

Use the Pythagorean Theorem to find the length of the height:
Plugging in our values, we get:
Example Question #2 : How To Find The Area Of A Trapezoid
Find the area of the following trapezoid:

The formula for the area of a trapezoid is

where 

Use the formula for a 
Use the formula for a 
Plugging in our values, we get:
Example Question #291 : Geometry
What is the area of this regular trapezoid?

45
20
32
26
32
To solve this question, you must divide the trapezoid into a rectangle and two right triangles. Using the Pythagorean Theorem, you would calculate the height of the triangle which is 4. The dimensions of the rectangle are 5 and 4, hence the area will be 20. The base of the triangle is 3 and the height of the triangle is 4. The area of one triangle is 6. Hence the total area will be 20+6+6=32. If you forget to split the shape into a rectangle and TWO triangles, or if you add the dimensions of the trapezoid, you could arrive at 26 as your answer.
Example Question #1 : How To Find The Area Of A Trapezoid

What is the area of the trapezoid above if a = 2, b = 6, and h = 4?
16
32
24
8
64
16
Area of a Trapezoid = ½(a+b)*h
= ½ (2+6) * 4
= ½ (8) * 4
= 4 * 4 = 16
Example Question #1 : Quadrilaterals
A trapezoid has a base of length 4, another base of length s, and a height of length s. A square has sides of length s. What is the value of s such that the area of the trapezoid and the area of the square are equal?
In general, the formula for the area of a trapezoid is (1/2)(a + b)(h), where a and b are the lengths of the bases, and h is the length of the height. Thus, we can write the area for the trapezoid given in the problem as follows:
area of trapezoid = (1/2)(4 + s)(s)
Similarly, the area of a square with sides of length a is given by a2. Thus, the area of the square given in the problem is s2.
We now can set the area of the trapezoid equal to the area of the square and solve for s.
(1/2)(4 + s)(s) = s2
Multiply both sides by 2 to eliminate the 1/2.
(4 + s)(s) = 2s2
Distribute the s on the left.
4s + s2 = 2s2
Subtract s2 from both sides.
4s = s2
Because s must be a positive number, we can divide both sides by s.
4 = s
This means the value of s must be 4.
The answer is 4.
Certified Tutor
Certified Tutor
All High School Math Resources

 .
.