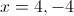We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Exponents

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 Next →

Example Question #1 : Solving And Graphing Exponential Equations

$y=\frac{3x^2-5}{2x^2+7}$

What are the horizontal asymptotes of this equation?

Possible Answers:

y=1

$y=\frac{2}{3}$

There are no horizontal asymptotes.

y=0

$y=\frac{3}{2}$

Correct answer:

$y=\frac{3}{2}$

Explanation:

Since the exponents of the variables in both the numerator and denominator are equal, the horizontal asymptote will be the coefficient of the numerator's variable divided by the coefficient of the denominator's variable.

For this problem, since we have $\frac{3x^2}{2x^2}$ , our asymptote will be $y=\frac{3}{2}$ .

Report an Error

Example Question #111 : Algebra Ii

$y=\frac{3x^2-5}{2x^2+7}$

What are the vertical asymptotes of the equation?

Possible Answers:

There are no real vertical asymptotes.

$x=-\sqrt{\frac{7}{2}}, \sqrt{\frac{7}{2}}$

$x=\frac{7}{2}$

There are no vertical asymptotes.

$x=-\sqrt{\frac{7}{2}}$

Correct answer:

There are no real vertical asymptotes.

Explanation:

To find the vertical asymptotes, we set the denominator equal to zero and solve.

$0={2x^2+7}$

-7=2x^2

$\frac{-7}{2}=x^2$

$\sqrt{-\frac{7}{2}}=\sqrt{x^2}$

$\sqrt{-\frac{7}{2}}=x$

Since we'd be trying to find a negative number, we have no real solution. Therefore, there are no real vertical asymptotes.

Report an Error

Example Question #21 : Exponents

$y=\frac{x^2-64}{x+2}$

What are the vertical asymptotes of this equation?

Possible Answers:

There are no real vertical asymptotes for this function.

x=2,-2

x=8,-8

x=-2

x=0

Correct answer:

x=-2

Explanation:

To find the vertical asymptotes, we set the denominator equal to zero.

0=x+2

-2=x

Report an Error

Example Question #1 : Solving And Graphing Exponential Equations

$y=\frac{x^2-9}{x^2-16}$

What is the horizontal asymptote of this equation?

Possible Answers:

y=3

y=0

There is no horizontal asymptote.

y=2

y=1

Correct answer:

y=1

Explanation:

Look at the exponents of the variables. Both our numerator and denominator are 1x^2 . Therefore the horizontal asymptote is calculated by dividing the coefficient of the numerator by the coefficient of the denomenator.

$y=\frac{1}{1}=1$

Report an Error

Example Question #10 : Solving And Graphing Exponential Equations

Find the vertical asymptote(s) of $y=\frac{x^2+9x+8}{x^2-44}$ .

Possible Answers:

x=1

There are no real vertical asymptotes for this function.

x=-1 and x=-8

$x=2\sqrt{11}$ and $x=-2\sqrt{11}$

$x=2\sqrt{11}$

Correct answer:

$x=2\sqrt{11}$ and $x=-2\sqrt{11}$

Explanation:

To find the vertical asymptotes, we set the denominator of the fraction equal to zero, as dividing anything by zero is undefined.

Take our given equation, $y=\frac{x^2+9x+8}{x^2-44}$ , and now set the denominator equal to zero:

0=x^2-44

44=x^2

$\sqrt{44}=\sqrt{x^2}$

is not a perfect square, but let's see if we can pull anything out.

$\sqrt{4*11}=\sqrt{x^2}$

$\sqrt{4}*\sqrt{11}=\sqrt{x^2}$

$2\sqrt{11}=x$

Don't forget that there is a negative result as well:

$x=-2\sqrt{11}$ .

Report an Error

Example Question #21 : Exponents

Find the vertical asymptote(s) of $y=\frac{x^3+2x+8}{x^2-36}$ .

Possible Answers:

x=6

x=36

There are no real vertical asymptotes.

x=-6 and x=6

$x=\frac{3}{2}$

Correct answer:

x=-6 and x=6

Explanation:

To find the vertical asymptotes, we set the denominator of the fraction equal to zero, as dividing anything by zero is "undefined." Since it's undefined, there's no way for us to graph that point!

Take our given equation, $y=\frac{x^3+2x+8}{x^2-36}$ , and now set the denominator equal to zero:

0=x^2-36 .

36=x^2

$\sqrt{36}=\sqrt{x^2}$

Don't forget, the root of a positive number can be both positive or negative ( -6^2=36 as does 6^2 ), so our answer will be $\pm6=x$ .

Therefore the vertical asymptotes are at x=-6 and x=6 .

Report an Error

Example Question #121 : Algebra Ii

Find the horizontal asymptote(s) of $y=\frac{x^3+2x+8}{x^2-36}$ .

Possible Answers:

y=1

There are no real horizontal asymptotes.

y=0

y=6 and y=-6

$y=\frac{3}{2}$

Correct answer:

There are no real horizontal asymptotes.

Explanation:

To find the horizontal asymptote of the function, look at the variable with the highest exponent. In the case of our equation, $y=\frac{x^3+2x+8}{x^2-36}$ , the highest exponent is x^3 in the numerator.

When the variable with the highest exponent is in the numberator, there are NO horizontal asymptotes. Horizontal asymptotes only appear when the greatest exponent is in the denominator OR when the exponents have same power in both the denominator and numerator.

Report an Error

Example Question #1 : Quadratic Functions

What are the -intercepts of the equation?

$y=\frac{x^2-9}{x^2-16}$

Possible Answers:

x=3

x=3,-3

x=2

x=4,-4

There are no -intercepts.

Correct answer:

x=3,-3

Explanation:

To find the x-intercepts of the equation, we set the numerator equal to zero.

0=x^2-9

9=x^2

$\sqrt{9}=\sqrt{x^2}$

3,-3=x

Report an Error

Example Question #3 : Find The Equations Of Vertical Asymptotes Of Tangent, Cosecant, Secant, And Cotangent Functions

Find the vertical asymptote of the equation.

$y=\frac{x^2-9}{x^2-16}$

Possible Answers:

x=4, -4

x=1

x=0

x=4

There are no vertical asymptotes.

Correct answer:

x=4, -4

Explanation:

To find the vertical asymptotes, we set the denominator of the function equal to zero and solve.

0=x^2-16

16=x^2

$\sqrt{16}=\sqrt{x^2}$

4, -4=x

Report an Error

Example Question #1311 : High School Math

$y=\frac{x^2-64}{x+2}$

What is the horizontal asymptote of this equation?

Possible Answers:

There is no horizontal asymptote.

y=0

y=1

y=-2

y=32

Correct answer:

There is no horizontal asymptote.

Explanation:

Since the exponent of the leading term in the numerator is greater than the exponent of the leading term in the denominator, there is no horizontal asymptote.

Report an Error

← Previous 1 2 3 4 5 6 Next →

View Tutors

David
Certified Tutor

Rhode Island College, Bachelor in Arts, English. Rhode Island College, Masters in Education, English.

View Tutors

Justin
Certified Tutor

University of Washington-Seattle Campus, Current Undergrad Student, Biomedical Engineering.

View Tutors

Raphael
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Computer Science.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Houston, Chemistry Tutors in Atlanta, Statistics Tutors in San Diego, Math Tutors in Dallas Fort Worth, LSAT Tutors in Denver, LSAT Tutors in San Francisco-Bay Area, French Tutors in Denver, Spanish Tutors in Dallas Fort Worth, Computer Science Tutors in Phoenix, MCAT Tutors in Chicago

Popular Courses & Classes

GMAT Courses & Classes in Houston, GMAT Courses & Classes in Denver, MCAT Courses & Classes in Chicago, MCAT Courses & Classes in Seattle, LSAT Courses & Classes in Denver, LSAT Courses & Classes in San Diego, GMAT Courses & Classes in Phoenix, ISEE Courses & Classes in Houston, GRE Courses & Classes in Washington DC, SSAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

SSAT Test Prep in Los Angeles, SAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Boston, SSAT Test Prep in New York City, GMAT Test Prep in Los Angeles, MCAT Test Prep in Los Angeles, GRE Test Prep in Miami, SSAT Test Prep in Philadelphia, MCAT Test Prep in Chicago, GMAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Exponents

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Solving And Graphing Exponential Equations

Example Question #111 : Algebra Ii

Example Question #21 : Exponents

Example Question #1 : Solving And Graphing Exponential Equations

Example Question #10 : Solving And Graphing Exponential Equations

Example Question #21 : Exponents

Example Question #121 : Algebra Ii

Example Question #1 : Quadratic Functions

Example Question #3 : Find The Equations Of Vertical Asymptotes Of Tangent, Cosecant, Secant, And Cotangent Functions

Example Question #1311 : High School Math

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: