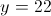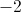High School Math : Parallel Lines
Study concepts, example questions & explanations for High School Math
All High School Math Resources
Example Questions
Example Question #41 : Lines
Which of these lines is parallel to 
Lines are parallel if they have the same slope. In standard 
For our given equation, the slope is 
Example Question #42 : Lines
Which of the following lines is parallel to 
Two lines that are parallel have the same slope. The slope of 
Example Question #3 : Parallel Lines
Which of these lines is parallel to 
Lines are parallel if they have the same slope. In standard 
For our given equation, the slope is 
Example Question #43 : Lines
Which of the following lines will be parallel to 
Two lines are parallel if they have the same slope. When a line is in standard 
For the given line 
Example Question #1 : Parallel Lines
Are the following lines parallel?
No
It cannot be determined from the information given
Yes
No
By definition, two lines are parallel if they have the same slope. Notice that since we are given the lines in the 
Example Question #4 : Parallel Lines
Which of the following lines is parallel to the line 
Parallel lines have the same slope. In slope-intercept form, 
Here the slope is 
Only one answer choice satisfies this requirement:
Note: the answer choice 
Example Question #1 : How To Find The Slope Of Parallel Lines
Which of the following lines would be parallel to the line described by the equation?
The way to determine parallel lines is to look at the slope. That means when you look at the equation in slope-intercept form, 
In the given problem, the slope is 
Example Question #1 : How To Find The Slope Of Parallel Lines
Which of the following lines would be parallel to 
Two lines are parallel if they have the same slope. When looking at the standard line equation 
Example Question #2 : How To Find The Slope Of Parallel Lines
What is the slope of the line that runs through points 
Use the slope formula (difference between 
Example Question #6 : Parallel Lines
A line that is parallel to 
Two lines that are parallel have the same slope. The line given above is in slope-intercept form, 
All High School Math Resources
