Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : How to find the surface area of a polyhedron

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Other Polyhedrons

Find the surface area of the following half-cylinder.

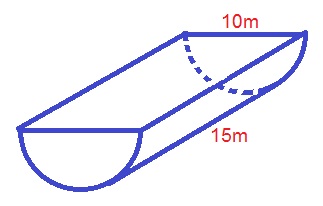
Half_cylinder

Possible Answers:

$110 \pi m^2$

$150+100 \pi m^2$

$75\pi m^2$

$50+125 \pi m^2$

$90 \pi m^2$

Correct answer:

$150+100 \pi m^2$

Explanation:

The formula for the surface area of a half-cylinder must include one-half of the surface area of a cylinder, which would be:

$SA = \frac{1}{2} (lateral\ area + 2 \cdot (base))$

We also need to add the area of the new rectangular face that is created by cutting the cylinder in half. The area of this rectangle would be:

$A=l\times w$

where the length of the rectangle is the same as the height of the half-cylinder, and the width of the rectangle is the same as the diameter of the base of the half-cylinder. So we can rewrite the area of the rectangle as:

$A=h\p\times d$

Now we can combine the two area formulas to find the total surface area of the half-cylinder:

$SA = \frac{1}{2} (2 \pi r (h) + 2 (\pi r^2))+h\cdot d$

$SA = \pi r (h) + \pi r^2+hd$

where is the radius of the base and is the length of the height, and is the diameter of the base.

Plugging in our values, we get:

$SA = \pi (5m) (15m) + \pi (5m)^2+15\cdot 10$

$SA = 75 \pi m^2 + 25 \pi m^2+150 = 150+100 \pi m^2$

Report an Error

Example Question #1 : How To Find The Surface Area Of A Polyhedron

Find the surface area of the following polyhedron.

Ice_cream_cone

Possible Answers:

$108 \pi m^2$

$88 \pi m^2$

$118 \pi m^2$

$98 \pi m^2$

$128 \pi m^2$

Correct answer:

$108 \pi m^2$

Explanation:

The formula for the surface area of the polyhedron is:

$SA = SA_{cone}+\frac{1}{2}SA_{sphere}$

$SA = \pi r l+\frac{1}{2}(4 \pi r^2)$

$SA = \pi r l+2 \pi r^2$

Where is the radius of the cone, is the slant height of the cone, and is the radius of the sphere

Use the formula for a 30-60-90 triangle to find the radius and slant height:

$a-a\sqrt{2}-2a$

$3\sqrt{3}m-9m-6\sqrt{3}m$

Plugging in our values, we get:

$SA = \pi r l+2 \pi r^2$

$SA = (\pi)(3\sqrt{3}m)(6\sqrt{3}m)+2(\pi)(3\sqrt{3}m)^2$

$SA = 54 \pi m^2 + 54 \pi m^2 = 108 \pi m^2$

Report an Error

Example Question #1 : How To Find The Surface Area Of A Polyhedron

Find the surface area of the following polyhedron.

Dome

Possible Answers:

$101 \pi m^2$

$71 \pi m^2$

$91 \pi m^2$

$61 \pi m^2$

$81 \pi m^2$

Correct answer:

$81 \pi m^2$

Explanation:

The formula for the surface area of the polyhedron is:

$SA = (cone:no\ base)+(cylinder:one\ base)$

$SA = \frac{1}{2}(circumference)(slant\ height)+(base)+(circumference)(height)$

$SA = \frac{1}{2}(2 \pi r)(h_s)+(\pi r^2)+(2 \pi r)(h)$

where is the radius of the cone, h_s is the slant height of the cone, is the radius of the cylinder, and is the height of the cylinder.

Use the formula for a 30-60-90 triangle to find the length of the radius:

$a-a\sqrt{3}-2a$

$3m-3\sqrt{3}m-6m$

Plugging in our values, we get:

$SA = \frac{1}{2}(2\pi (3m))(6m)+(\pi)(3m)^2+(2\pi (3m)(9m))$

$SA = 81 \pi m^2$

Report an Error

Example Question #1 : How To Find The Surface Area Of A Polyhedron

Find the surface area of the following polyhedron.

Ice_cream_cone

Possible Answers:

$32\sqrt{2}\pi + 32 \pi m^2$

$64\sqrt{2}\pi + 32 \pi m^2$

$32\sqrt{2}\pi + 64 \pi m^2$

$64\sqrt{2}\pi + 64 \pi m^2$

Correct answer:

$32\sqrt{2}\pi + 64 \pi m^2$

Explanation:

The formula for the surface area of a polyhedron is:

$SA = (cone)+ \frac{1}{2}(sphere)$

$SA = \frac{1}{2}(2\pi r)(h_s)+ \frac{1}{2}(4\pi r^2)$

$SA = \pi rh_s+ 2\pi r^2$

where is the radius of the polyhedron and h_s is the slant height of the cone.

Use the formula for a 45-45-90 triangle to find the length of the radius:

$a-a-a\sqrt{2}$

$4\sqrt{2}m-4\sqrt{2}m-8m$

Plugging in our values, we get:

$SA = \pi (4\sqrt{2}m)(8m)+ 2\pi (4\sqrt{2}m)^2$

$SA = 32\sqrt{2}\pi + 64 \pi m^2$

Report an Error

View Tutors

Aaron
Certified Tutor

University of Dallas, Bachelor of Science, Chemistry. Texas A & M University-College Station, Doctor of Philosophy, Nuclear E...

1743201268 mini magick20250328 178 17dmuet

View Tutors

Zoe
Certified Tutor

Walla Walla University, Bachelor of Science, Elementary School Teaching.

View Tutors

Ana Marie
Certified Tutor

Cebu Normal University, Bachelor of Science, Mathematics.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in San Diego, Biology Tutors in San Francisco-Bay Area, SSAT Tutors in Seattle, French Tutors in San Francisco-Bay Area, Chemistry Tutors in Chicago, GMAT Tutors in Denver, French Tutors in Phoenix, ISEE Tutors in Chicago, English Tutors in Phoenix, Computer Science Tutors in Houston

Popular Courses & Classes

MCAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Washington DC, ACT Courses & Classes in San Diego, MCAT Courses & Classes in Philadelphia, LSAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Atlanta, ISEE Courses & Classes in Seattle, GRE Courses & Classes in Houston, GRE Courses & Classes in New York City, LSAT Courses & Classes in Miami

Popular Test Prep

LSAT Test Prep in Denver, SAT Test Prep in Houston, GRE Test Prep in Houston, ACT Test Prep in Washington DC, LSAT Test Prep in Chicago, ACT Test Prep in San Diego, LSAT Test Prep in Miami, MCAT Test Prep in Houston, GRE Test Prep in Philadelphia, GMAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : How to find the surface area of a polyhedron

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Other Polyhedrons

Example Question #1 : How To Find The Surface Area Of A Polyhedron

Example Question #1 : How To Find The Surface Area Of A Polyhedron

Example Question #1 : How To Find The Surface Area Of A Polyhedron

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: