All High School Math Resources
Example Questions
Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle
The lengths of two sides of a triangle are 9 and 7. Which of the following could be the length of the third side?
17
12
1
16
2
12
Let us call the third side x. According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be larger than the other two sides. Thus, all of the following must be true:
x + 7 > 9
x + 9 > 7
7 + 9 > x
We can solve these three inequalities to determine the possible values of x.
x + 7 > 9
Subtract 7 from both sides.
x > 2
Now, we can look at x + 9 > 7. Subtracting 9 from both sides, we obtain
x > –2
Finally, 7 + 9 > x, which means that 16 > x.
Therefore, x must be greater than 2, greater than –2, but also less than 16. The only number that satisfies all of these requirements is 12.
The answer is 12.
Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle
The lengths of a triangle are 8, 12, and x. Which of the following inequalities shows all of the possible values of x?
4 < x <12
4 ≤ x ≤12
4 ≤ x ≤ 20
8 < x < 12
4 < x < 20
4 < x < 20
According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be greater (not greater than or equal) than the remaining side. Thus, the following inequalities must all be true:
x + 8 > 12
x + 12 > 8
8 + 12 > x
Let's solve each inequality.
x + 8 > 12
Subtract 8 from both sides.
x > 4
Next, let's look at the inequality x + 12 > 8
x + 12 > 8
Subtract 12 from both sides.
x > –4
Lastly, 8 + 12 > x, which means that x < 20.
This means that x must be less than twenty, but greater than 4 and greater than –4. Since any number greater than 4 is also greater than –4, we can exclude the inequality x > –4.
To summarize, x must be greater than 4 and less than 20. We can write this as 4 < x < 20.
The answer is 4 < x < 20.
Example Question #131 : Triangles
If 2 sides of the triangle are have lengths equal to 8 and 14, what is one possible length of the third side?
20
Not enough information
22
6
4
20
The sum of the lengths of 2 sides of a triangle must be greater than—but not equal to—the length of the third side. Further, the third side must be longer than the difference between the greater and the lesser of the other two sides; therefore, 20 is the only possible answer.
Example Question #122 : Triangles
In 
13
17
11
9
10
11
Rule - the length of one side of a triangle must be greater than the differnce and less than the sum of the lengths of the other two sides.
Given lengths of two of the sides of the 
The question asks what is the least possible integer length of BC, which would be 11
Example Question #132 : Triangles
Two sides of a triangle have lengths 4 and 7. Which of the following represents the set of all possible lengths of the third side, x?
3 < x < 11
4 < x < 11
3 < x < 7
2 < x < 12
4 < x < 7
3 < x < 11
The set of possible lengths is: 7-4 < x < 7+4, or 3 < X < 11.
Example Question #133 : Triangles
If two sides of a triangle have lengths 8 and 10, what could the length of the third side NOT be?
14
8
10
19
5
19
According to the Triangle Inequality Theorem, the sums of the lengths of any two sides of a triangle must be greater than the length of the third side. Since 10 + 8 is 18, the only length out of the answer choices that is not possible is 19.
Example Question #1 : How To Find If Two Acute / Obtuse Triangles Are Similar
Are the triangles similar? If so, solve for 

The triangles are not similar
Yes;
Yes;
Yes;
Yes;
The triangles are similar because of the side-angle-side postulate.
Side:
Angle:
Side:
The third side must also have a 2:3 ratio.
Cross-multiply, and solve for 
Example Question #2 : How To Find If Two Acute / Obtuse Triangles Are Similar
Are the triangles similar? If so, solve for 
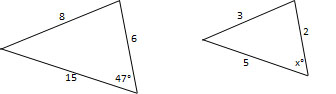
Yes;
Yes;
Yes;
The triangles are not similar
The triangles are not similar
The triangles are not similar, as proven by the side-side-side postulate.
The third side does not follow the same ratio of the other two, thus the triangles are not similar.
Example Question #1 : How To Find If Two Acute / Obtuse Triangles Are Similar


The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.
Perimeter A = 45” and perimeter B = 135”
The proportion of Perimeter A to Perimeter B is 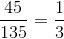
This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.
15” x 3 = 45”
10” x 3 = 30“

Example Question #1 : How To Find If Two Acute / Obtuse Triangles Are Similar
Side-Side-Angle Postulate
Angle-Angle Postulate
Side-Angle-Side Postulate
Side-Side-Side Postulate
Angle-Angle Postulate
Angle-Angle Postulate: if two angles of one triangle are equal to two corresponding angles of another triangle, the triangles must be similar.
In this example, the triangles share one angle, which must be equal. Additionally, the triangles contain segments that are parallel to each other. When two parallel lines are crossed by another line, the corresponding angles must be equal. Each angle in one triangle is congruent with its corresponding angle in the other triangle, indicating that they are similar.
All High School Math Resources




























