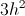We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #13 : Isosceles Triangles

An isosceles triangle has an area of 12. If the ratio of the base to the height is 3:2, what is the length of the two equal sides?

Possible Answers:

4√3

3√3

Correct answer:

Explanation:

Area of a triangle is ½ x base x height. Since base:height = 3:2, base = 1.5 height. Area = 12 = ½ x 1.5 height x height or 24/1.5 = height². Height = 4. Base = 1.5 height = 6. Half the base and the height form the legs of a right triangle, with an equal leg of the isosceles triangle as the hypotenuse. This is a 3-4-5 right triangle.

Sat_math_167_01

Report an Error

Example Question #62 : Triangles

Two sides of a triangle each have length 6. All of the following could be the length of the third side EXCEPT

Possible Answers:

Correct answer: 12

Explanation:

This question is about the Triangle Inequality, which states that in a triangle with two sides A and B, the third side must be greater than the absolute value of the difference between A and B and smaller than the sum of A and B.

Applying the Triangle Inequality to this problem, we see that the third side must be greater than the absolute value of the difference between the other two sides, which is |6-6|=0, and smaller than the sum of the two other sides, which is 6+6=12. The only answer choice that does not satisfy this range of possible values is 12 since the third side must be LESS than 12.

Report an Error

Example Question #62 : Triangles

Find the area of a triangle whose base is 14in and whose height is 2ft .

Possible Answers:

$336in ^{2}$

$168in^{2}$

$196in^{2}$

$186in^{2}$

$136in^{2}$

Correct answer:

$168in^{2}$

Explanation:

This problem is solved using the geometric formula for the area of a triangle.

$A=\frac{1}{2}b*h$

Convert feet to inches.

$\dpi{100} \frac{2ft}{1}*\frac{12in}{1ft}=24in$

$A=\frac{1}{2}*14in*24in$

$A=168in^{2}$

Report an Error

Example Question #335 : Plane Geometry

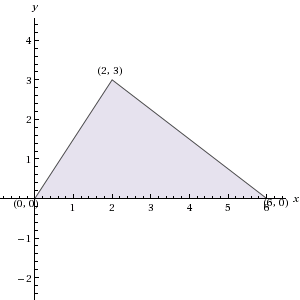
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?

Possible Answers:

Correct answer:

Explanation:

Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.

Report an Error

Example Question #61 : Triangles

What is the area of a triangle with a height of and a base of ?

Possible Answers:

Correct answer:

Explanation:

When searching for the area of a triangle we are looking for the amount of the space enclosed by the triangle.

The equation for area of a triangle is

Plug the values for base and height into the equation yielding

$\frac{1}{2}(4)(7)=Area$

Then multiply the numbers together to arrive at the answer .

Report an Error

Example Question #871 : High School Math

The height, , of triangle PQR in the figure is one-fourth the length of . In terms of h, what is the area of triangle PQR ?

Possible Answers:

$3h^{2}$

$2h^{2}$

$h^{2}$

$\frac{1}{2}h^{2}$

Correct answer:

$2h^{2}$

Explanation:

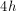
If $\dpi{100} \small h=\frac{1}{4}$ * $\dpi{100} \small \overline{PQ}$ , then the length of $\dpi{100} \small \overline{PQ}$ must be $\dpi{100} \small 4h$ .

Using the formula for the area of a triangle ( $\frac{1}{2}bh$ ), with $\dpi{100} \small b=4h$ , the area of the triangle must be $2h^{2}$ .

Report an Error

Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

A triangle has a perimeter of 36 inches, and one side that is 12 inches long. The lengths of the other two sides have a ratio of 3:5. What is the length of the longest side of the triangle?

Possible Answers:

Correct answer:

Explanation:

We know that the perimeter is 36 inches, and one side is 12. This means, the sum of the lengths of the other two sides are 24. The ratio between the two sides is 3:5, giving a total of 8 parts. We divide the remaining length, 24 inches, by 8 giving us 3. This means each part is 3. We multiply this by the ratio and get 9:15, meaning the longest side is 15 inches.

Report an Error

Example Question #71 : Triangles

A triangle has sides of length 8, 13, and L. Which of the following cannot equal L?

Possible Answers:

Correct answer:

Explanation:

The sum of the lengths of two sides of a triangle cannot be less than the length of the third side. 8 + 4 = 12, which is less than 13.

Report an Error

Example Question #2 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

Two sides of a triangle are 20 and 32. Which of the following CANNOT be the third side of this triangle.

Possible Answers:

Correct answer:

Explanation:

Please remember the Triangle Inequality Theorem, which states that the sum of any two sides of a triangle must be greater than the third side. Therefore, the correct answer is 10 because the sum of 10 and 20 would not be greater than the third side 32.

Report an Error

Example Question #146 : Sat Mathematics

A triangle has sides of length 5, 7, and x. Which of the following can NOT be a value of x?

Possible Answers:

Correct answer:

Explanation:

The sum of the lengths of any two sides of a triangle must exceed the length of the third side; therefore, 5+7 > x, which cannot happen if x = 13.

Report an Error

View Tutors

Jennifer
Certified Tutor

North Carolina State University at Raleigh, Bachelor of Science, Zoology.

View Tutors

Justin
Certified Tutor

University of Rhode Island, Master of Science, Industrial Engineering.

View Tutors

Lindsey
Certified Tutor

Pittsburgh Institute of Mortuary Science Inc, Bachelor of Science, Funeral Service and Mortuary Science.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Seattle, English Tutors in Denver, Computer Science Tutors in Atlanta, LSAT Tutors in San Diego, Biology Tutors in San Francisco-Bay Area, Math Tutors in Atlanta, Spanish Tutors in San Diego, English Tutors in Washington DC, Chemistry Tutors in Philadelphia, Algebra Tutors in Houston

Popular Courses & Classes

ACT Courses & Classes in Atlanta, ISEE Courses & Classes in Washington DC, GMAT Courses & Classes in Atlanta, ISEE Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Seattle, SAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Miami, SSAT Courses & Classes in Atlanta

Popular Test Prep

GMAT Test Prep in Philadelphia, LSAT Test Prep in Miami, GRE Test Prep in Chicago, GMAT Test Prep in Denver, ISEE Test Prep in Washington DC, ISEE Test Prep in Dallas Fort Worth, MCAT Test Prep in Houston, ACT Test Prep in Houston, GMAT Test Prep in Dallas Fort Worth, GRE Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #13 : Isosceles Triangles

Example Question #62 : Triangles

Example Question #62 : Triangles

Example Question #335 : Plane Geometry

Example Question #61 : Triangles

Example Question #871 : High School Math

Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

Example Question #71 : Triangles

Example Question #2 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

Example Question #146 : Sat Mathematics

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: