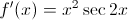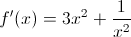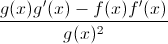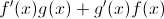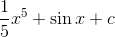Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #64 : Derivatives

What is the second derivative of $\sin(x)$ ?

Possible Answers:

$\sec(x)$

$-\cos(x)$

$\cos(x)$

$-\sin(x)$

$\csc(x)$

Correct answer:

$-\sin(x)$

Explanation:

The derivatives of trig functions must be memorized. The first derivative is:

$\frac{\mathrm{d} }{\mathrm{d} x}\sin(x)=\cos(x)$ .

To find the second derivative, we take the derivative of our result.

$\frac{\mathrm{d} }{\mathrm{d} x}\cos(x)=-\sin(x)$ .

Therefore, the second derivative will be $-\sin(x)$ .

Report an Error

Example Question #65 : Derivatives

Compute the derivative of the function $f(x) = \tan x^{2}$ .

Possible Answers:

$f' (x) = x^{2} \tan x^{2} + 2x \sec^{2} x^{2}$

$f' (x) = 2x \sec x^{2}$

$f' (x) = 2x \sec^{2} x^{2}$

$f' (x) = x^{2} \sec^{2} x^{2}$

$f' (x) = x^{2} \sec 2x$

Correct answer:

$f' (x) = 2x \sec^{2} x^{2}$

Explanation:

Use the Chain Rule.

Set $u = x^{2}$ and substitute.

$f(x) = \tan u$

$\frac{\mathrm{d} f }{\mathrm{d} u} = \frac{\mathrm{d} }{\mathrm{d} u} \tan u = \sec^{2} u$

$\frac{\mathrm{d} u }{\mathrm{d} x} = \frac{\mathrm{d} }{\mathrm{d} x} x^{2} = 2x^{2-1} =2x$

$\frac{\mathrm{d} f }{\mathrm{d} x} = \frac{\mathrm{d} f }{\mathrm{d} u} \cdot \frac{\mathrm{d} u }{\mathrm{d} x}= \sec^{2} u \cdot 2x = 2x \sec^{2} x^{2}$

Report an Error

Example Question #1 : Understanding Derivatives Of Sums, Quotients, And Products

Find the derivative of the following function:

$f(x) = x^3 + \frac{1}{x}$

Possible Answers:

$f'(x) = 3x^2-\frac{1}{x^2}$

f'(x) = 3x^2

f'(x) = 3x^2+x

$f'(x) = 3x^2+\frac{1}{x^2}$

$f'(x) = 3x^2-\frac{1}{x}$

Correct answer:

$f'(x) = 3x^2-\frac{1}{x^2}$

Explanation:

Since this function is a polynomial, we take the derivative of each term separately.

From the power rule, the derivative of

x^3

is simply

3x^2

We can rewrite $\frac{1}{x}$ as

$x^{-1}$

and using the power rule again, we get a derivative of

$-x^{-2}$ or $-\frac{1}{x^2}$

So the answer is

$f'(x) = 3x^2-\frac{1}{x^2}$

Report an Error

Example Question #2 : Understanding Derivatives Of Sums, Quotients, And Products

What is $\frac{\mathrm{d} }{\mathrm{d} x}f(x)*g(x)\mathrm{d x} ?$

Possible Answers:

f(x)g'(x)+f'(x)g(x)

f(x)*f'(x)+g(x)*g'(x)

$\frac{g(x)f'(x)-f(x)g'(x)}{g(x)^2}$

f(x)g(x)+f'(x)g'(x)

f(x)g'(x)-f'(x)g(x)

Correct answer:

f(x)g'(x)+f'(x)g(x)

Explanation:

The chain rule is "first times the derivative of the second plus second times derivative of the first".

In this case, that means $\frac{\mathrm{d} }{\mathrm{d} x}f(x)*g(x)\mathrm{d x} =f(x)g'(x)+f'(x)g(x)$ .

Report an Error

Example Question #2 : Understanding Derivatives Of Sums, Quotients, And Products

What is the first derivative of $5x^4+\sin x$ ?

Possible Answers:

$20x^3+\frac{1}{\sin x}$

$20x^{3}-\cos x$

$5x^4\cos x +20x^3\sin x$

$20x^3+4\cos x$

$20x^{3}+\cos x$

Correct answer:

$20x^{3}+\cos x$

Explanation:

Since we're adding terms, we take the derivative of each part separately. For 5x^4 , we can use the power rule, which states that we multiply the variable by the current exponent and then lower the exponent by one. For sine, we use our trigonometric derivative rules.

Remember, $\frac{\mathrm{d} }{\mathrm{d} x} \sin x=\cos x$ .

$\frac{\mathrm{d} }{\mathrm{d} x}5x^4+\sin x=(4*5x^{4-1})+\cos x$

$\frac{\mathrm{d} }{\mathrm{d} x}5x^4+\sin x=(20x^{3})+\cos x$

Report an Error

Example Question #83 : Calculus I — Derivatives

What is the second derivative of $5x^4+\sin x$ ?

Possible Answers:

$40x^2-\cos x$

$60x^{2}-\sin x$

$40x^{2}-\sin x$

$x^5-\csc x$

$120x+\sin x$

Correct answer:

$60x^{2}-\sin x$

Explanation:

To find the second derivative, we need to start by finding the first one.

Remember, $\frac{\mathrm{d} }{\mathrm{d} x} \sin x=\cos x$ .

$\frac{\mathrm{d} }{\mathrm{d} x}5x^4+\sin x=(4*5x^{4-1})+\cos x$

$\frac{\mathrm{d} }{\mathrm{d} x}5x^4+\sin x=(20x^{3})+\cos x$

Now we repeat the process, but using $20x^3+\cos x$ as our equation.

$\frac{\mathrm{d} }{\mathrm{d} x} \cos x=-\sin x$

$\frac{\mathrm{d} }{\mathrm{d} x}20x^3+\cos x=(3*20x^{3-1})-\sin x$

$\frac{\mathrm{d} }{\mathrm{d} x}20x^3+\cos x=(60x^{2})-\sin x$

Report an Error

Example Question #3 : Understanding Derivatives Of Sums, Quotients, And Products

Which of the following best represents $\frac{\mathrm{d} }{\mathrm{d} x}\frac{f(x)}{g(x)}$ ?

Possible Answers:

$\frac{f'(x)}{g'(x)}$

$\frac{g(x)f'(x)-f(x)g'(x)}{g(x)^2}$

$\frac{g(x)g'(x)-f(x)f'(x)}{g(x)^2}$

f'(x)g(x)+g'(x)f(x)

$\frac{f(x)g'(x)-g(x)f'(x)}{g(x)^2}$

Correct answer:

$\frac{g(x)f'(x)-f(x)g'(x)}{g(x)^2}$

Explanation:

The question is just asking for the Quotient Rule formula.

Recall the Quotient Rule is the bottom function times the derivative of the top minus the top function times the derivative of the bottom all divided by the bottom function squared.

Given,

$\frac{\mathrm{d} }{\mathrm{d} x}\frac{f(x)}{g(x)}$

the bottom function is g(x) and the top function is f(x) . This makes the bottom derivative g'(x) and the top derivative f'(x) .

Substituting these into the Quotient Rule formula resulting in the following.

$\frac{\mathrm{d} }{\mathrm{d} x}\frac{f(x)}{g(x)}=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{(g(x))^2}$

Report an Error

Example Question #1 : Understanding Integrals Of Sums, Quotients, And Products

$\int 5x^4+\sin x\ {\mathrm{d} x}=?$

Possible Answers:

$\frac{1}{5}x^5+\sin x +c$

$5x^5+\cos x+c$

$(20 x^3-6x) *\sin(x)-(5x^4-60x^2+120)* \cos(x)+c$

$20x-\cos x$

$x^5-\cos x +c$

Correct answer:

$x^5-\cos x +c$

Explanation:

Since we're adding terms, we take the integral or anti-derivative of each part separately. For 5x^4 , we can use the reverse power rule, which states that we raise the exponent of the variable by one and then divide by that new exponent. For sine, we use our trigonometric integral rules.

Remember, $\int \sin x \ {\mathrm{d} x}=-\cos x$ .

$\int 5x^4+\sin x\ {\mathrm{d} x}= (\frac{5x^{4+1}}{4+1})+(-\cos x)+c$

Don't forget to include a + c to account for any constants!

$\int 5x^4+\sin x\ {\mathrm{d} x}= (\frac{5x^{5}}{5})+(-\cos x)+c$

$\int 5x^4+\sin x\ {\mathrm{d} x}=x^5-\cos x +c$

Report an Error

Example Question #1 : Using Limits With Continuity

Function

The above graph depicts a function h(x) . Does $\lim_{x\rightarrow 1} h(x)$ exist, and why or why not?

Possible Answers:

$\lim_{x\rightarrow 1} h(x)$ does not exist because $f (1 ) \neq \lim_{x\rightarrow 1^{+}} h(x)$

$\lim_{x\rightarrow 1} h(x)$ exists because $\lim_{x\rightarrow 1^{-}} | h(x)| = \lim_{x\rightarrow 1^{+}} |h(x)|$

$\lim_{x\rightarrow 1} h(x)$ does not exist because $\lim_{x\rightarrow 1^{-}} h(x) \neq \lim_{x\rightarrow 1^{+}} h(x)$ .

$\lim_{x\rightarrow 1} h(x)$ exists because $f (1 ) = \frac{\lim_{x\rightarrow 1^{-}} h(x) + \lim_{x\rightarrow 1^{+ }} h(x)}{2}$

$\lim_{x\rightarrow 1} h(x)$ does not exist because $f (1 ) \neq \lim_{x\rightarrow 1^{-}} h(x)$

Correct answer:

$\lim_{x\rightarrow 1} h(x)$ does not exist because $\lim_{x\rightarrow 1^{-}} h(x) \neq \lim_{x\rightarrow 1^{+}} h(x)$ .

Explanation:

$\lim_{x\rightarrow 1} h(x)$ exists if and only if $\lim_{x\rightarrow 1^{-}} h(x) = \lim_{x\rightarrow 1^{+}} h(x)$ . As can be seen from the diagram, $\lim_{x\rightarrow 1^{-}} h(x) = 1$ , but $\lim_{x\rightarrow 1^{+}} h(x) = -1$ . Since $\lim_{x\rightarrow 1^{-}} h(x) \neq \lim_{x\rightarrow 1^{+}} h(x)$ , $\lim_{x\rightarrow 1} h(x)$ does not exist.

Report an Error

Example Question #2 : Using Limits With Continuity

Function

The above graph depicts a function f(x) . Does $\lim_{x\rightarrow 1} f(x)$ exist, and why or why not?

Possible Answers:

$\lim_{x\rightarrow 1} f(x)$ does not exist because $f(1) \neq \lim_{x\rightarrow 1^{-}} f(x)$

$\lim_{x\rightarrow 1} f(x)$ does not exist because is not continuaous at x = 1 .

$\lim_{x\rightarrow 1} f(x)$ exists because $\lim_{x\rightarrow 1^{+}} f(x) = \lim_{x\rightarrow 1^{-}} f(x)$

$\lim_{x\rightarrow 1} f(x)$ does not exist because $\lim_{x\rightarrow 1^{+}} f(x) \neq \lim_{x\rightarrow 1^{-}} f(x)$

$\lim_{x\rightarrow 1} f(x)$ does not exist because $f(1) \neq \lim_{x\rightarrow 1^{+}} f(x)$

Correct answer:

$\lim_{x\rightarrow 1} f(x)$ exists because $\lim_{x\rightarrow 1^{+}} f(x) = \lim_{x\rightarrow 1^{-}} f(x)$

Explanation:

$\lim_{x\rightarrow 1} f(x)$ exists if and only if $\lim_{x\rightarrow 1^{+}} f(x) = \lim_{x\rightarrow 1^{-}} f(x)$ ;

the actual value of f(1) is irrelevant, as is whether is continuous there.

As can be seen,

$\lim_{x\rightarrow 1^{+}} f(x) = 1$ and $\lim_{x\rightarrow 1^{-}} f(x) = 1$ ;

therefore, $\lim_{x\rightarrow 1^{+}} f(x) = \lim_{x\rightarrow 1^{-}} f(x)$ ,

and $\lim_{x\rightarrow 1} f(x)$ exists.

Report an Error

View Tutors

Kathryn
Certified Tutor

Georgia College & State University, Bachelor of Science, Foods, Nutrition, and Wellness Studies. Georgia State University, Ma...

View Tutors

Maria G.
Certified Tutor

Universidad del Valle de Mexico, Bachelor of Science, Manufacturing Engineering. Houston Baptist University, Masters in Educa...

View Tutors

Nicole
Certified Tutor

Liberty University, Bachelor of Science, Psychology. Liberty University, Master of Arts, Mental Health Counseling.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Seattle, Biology Tutors in Seattle, Biology Tutors in Chicago, SAT Tutors in Denver, Statistics Tutors in Chicago, Physics Tutors in Atlanta, ISEE Tutors in Atlanta, Calculus Tutors in Phoenix, MCAT Tutors in Denver, Chemistry Tutors in San Diego

Popular Courses & Classes

ACT Courses & Classes in Boston, GRE Courses & Classes in Denver, ISEE Courses & Classes in Atlanta, GMAT Courses & Classes in Chicago, SAT Courses & Classes in Boston, GRE Courses & Classes in Phoenix, GMAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Chicago, ISEE Courses & Classes in Los Angeles, SSAT Courses & Classes in New York City

Popular Test Prep

SAT Test Prep in Phoenix, GMAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Boston, ACT Test Prep in Philadelphia, SAT Test Prep in Chicago, LSAT Test Prep in Denver, ISEE Test Prep in San Francisco-Bay Area, SSAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Phoenix, GMAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #64 : Derivatives

Example Question #65 : Derivatives

Example Question #1 : Understanding Derivatives Of Sums, Quotients, And Products

Example Question #2 : Understanding Derivatives Of Sums, Quotients, And Products

Example Question #2 : Understanding Derivatives Of Sums, Quotients, And Products

Example Question #83 : Calculus I — Derivatives

Example Question #3 : Understanding Derivatives Of Sums, Quotients, And Products

Example Question #1 : Understanding Integrals Of Sums, Quotients, And Products

Example Question #1 : Using Limits With Continuity

Example Question #2 : Using Limits With Continuity

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: