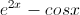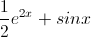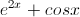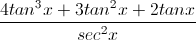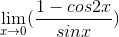All High School Math Resources
Example Questions
Example Question #1 : Derivatives
Find the second derivative of f(x).
First we should find the first derivative of 




The second derivative is just the derivative of the first derivative:
Example Question #2181 : High School Math
Find the derivative of the function

We can use the Chain Rule:
Let 

Example Question #2182 : High School Math
Evaluate the following limit:
When 



Example Question #32 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change
Evaluate:

Example Question #33 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change
Find
This is most easily solved by recognizing that 
Example Question #1 : Integrals
Remember the fundamental theorem of calculus!
Since our 
Remember to include the 
Now we can plug that equation into our FToC equation:
Notice that the c's cancel out. Plug in the given values for a and b and solve:
Example Question #2 : Integrals
Remember the fundamental theorem of calculus!
Since our 
Remember to include the 
Now we can plug that equation into our FToC equation:
Notice that the c's cancel out. Plug in the given values for a and b and solve:
Example Question #5 : Integrals
Remember the fundamental theorem of calculus!
As it turns out, since our 


Remember to include the 
Now we can plug that equation into our FToC equation:
Notice that the c's cancel out. Plug in the given values for a and b and solve:
Example Question #6 : Integrals
Remember the fundamental theorem of calculus!
As it turns out, since our 


Remember to include the 
Now we can plug that equation into our FToC equation:
Notice that the c's cancel out. Plug in the given values for a and b and solve:
Because 

Example Question #7 : Integrals
Remember the fundamental theorem of calculus!
Since our 
Remember to include the 
Now we can plug that equation into our FToC equation:
Notice that the c's cancel out. Plug in the given values for a and b and solve:
Certified Tutor
Certified Tutor
All High School Math Resources