All High School Math Resources
Example Questions
Example Question #2081 : High School Math
Calculate 
The limit does not exist.
Substitute 
(Note that as 



Example Question #23 : Limits Of Functions (Including One Sided Limits)
Calculate
The limit does not exist.
You can substitute 
Note that as 


Example Question #2 : Techniques Of Antidifferentiation
The speed of a car traveling on the highway is given by the following function of time:
Note that
What does this mean?
The car's speed is constantly changing at time 
The car is not decelerating at time 
The car is not moving at time 
The car takes 
The car is not accelerating at time 
The car is not moving at time 
The function 






Example Question #2082 : High School Math
The speed of a car traveling on the highway is given by the following function of time:
Consider a second function:
What can we conclude about this second function?
It represents the rate at which the speed of the car is changing.
It has no relation to the previous function.
It represents another way to write the car's speed.
It represents the change in distance over a given time 
It represents the total distance the car has traveled at time 
It represents the rate at which the speed of the car is changing.
Notice that the function 

Therefore, 
Example Question #1 : Derivatives
Define 
Give the interval(s) on which 

<0)
We need to find the values of 
&space;=&space;3x%5E%7B2%7D&space;-18x+24&space;<0)
These are the boundary points, so the intervals we need to check are:


We check each interval by substituting an arbitrary value from each for 
Choose

Choose

Choose

The answer is that 

Example Question #2 : Derivatives
Define &space;=&space;x%5E%7B3%7D&space;-&space;%5Cfrac%7B21%7D%7B2%7D&space;x%5E%7B2%7D&space;+30x&space;-6)
Give the interval(s) on which 

>0)
We need to find the values of 

These are the boundary points, so the intervals we need to check are:


We check each interval by substituting an arbitrary value from each for 
Choose

Choose

Choose

The answer is that 
Example Question #1 : Applications Of Derivatives
At what point does 
It does not shift from increasing to decreasing
To find out where the graph shifts from increasing to decreasing, we need to look at the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
We're going to treat 

Notice that 
If we were to graph 
Example Question #21 : Relationship Between The Increasing And Decreasing Behavior Of ƒ And The Sign Of ƒ'
At what point does 
To find out where it shifts from decreasing to increasing, we need to look at the first derivative. The shift will happen where the first derivative goes from a negative value to a positive value.
To find the first derivative for this problem, we can use the power rule. The power rule states that we lower the exponent of each of the variables by one and multiply by that original exponent.
Remember that anything to the zero power is one.
Can this equation be negative? Yes. Does it shift from negative to positive? Yes. Therefore, it will shift from negative to positive at the point that 
Example Question #2 : Applications Of Derivatives
At what value of 

It does not shift from decreasing to increasing
To find out when the function shifts from decreasing to increasing, we look at the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
Anything to the zero power is one.
From here, we want to know if there is a point at which graph changes from negative to positive. Plug in zero for y and solve for x.
This is the point where the graph shifts from decreasing to increasing.
Example Question #3 : Applications Of Derivatives
At the point 

Increasing, concave
Increasing, convex
Decreasing, concave
The function is undefined at that point
Decreasing, convex
Decreasing, convex
First, let's find out if the graph is increasing or decreasing. For that, we need the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
We're going to treat 

Notice that 
Plug in our given point for 
Our result is negative, therefore the function is decreasing.
To find the concavity, look at the second derivative. If the function is positive at our given point, it is concave. If the function is negative, it is convex.
To find the second derivative we repeat the process, but using 
As you can see, our second derivative is a constant. It doesn't matter what point we plug in for 
Combine our two pieces of information to see that at the given point, the graph is decreasing and convex.
All High School Math Resources





























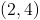
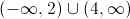

&space;=&space;3%5Ccdot&space;x%5E%7B3-1%7D&space;-2%5Ccdot&space;9x%5E%7B2-1%7D+24+0)























































































