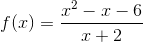All High School Math Resources
Example Questions
Example Question #11 : Sequences And Series
Find the sum of all even integers from 

The formula for the sum of an arithmetic series is

where 


We know that there are 


Example Question #21 : Sequences And Series
Find the sum of all even integers from 

The formula for the sum of an arithmetic series is

where 


Example Question #2063 : High School Math
Find the sum of the even integers from 

The sum of even integers represents an arithmetic series.
The formula for the partial sum of an arithmetic series is

where 


Plugging in our values, we get:
Example Question #191 : Pre Calculus
Find the value for
To best understand, let's write out the series. So
We can see this is an infinite geometric series with each successive term being multiplied by 
A definition you may wish to remember is





Example Question #31 : Sequences And Series
Evaluate:
The series does not converge.
This is a geometric series whose first term is 

Example Question #1 : Sums Of Infinite Series
Evaluate:
The series does not converge.
This is a geometric series whose first term is 

Example Question #1 : Understanding The Definition Of Limits
A limit describes what 

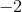


Substituting 

One method of finding the limit is to try and simplify the equation as much as possible:
As you can see, there are common factors between the numerator and the denominator that can be canceled out. (Remember, when you cancel out a factor from a rational equation, it means that the function has a hole -- an undefined point -- where that factor equals zero.)
After canceling out the common factors, we're left with:
Even though the domain of the original function is restricted (

Example Question #1 : Finding One Sided Limits
Let 
Find 
The limit does not exist.

This is a graph of 




This can be illustrated by thinking of small negative numbers.
NOTE: Pay attention to one-sided limit specifications, as it is easy to pick the wrong answer choice if you're not careful.

Example Question #51 : Pre Calculus
Evaluate the limit below:
0
1




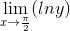

So, we can apply the L’ Hospital's Rule:
since:
hence:
Example Question #2061 : High School Math
Certified Tutor
Certified Tutor
All High School Math Resources