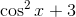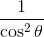We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Using Pythagorean Identities

Simplify:

$\sin^2x+\cos^2x+\tan^2x$

Possible Answers:

$\csc^2 x$

This is the most simplified version.

$\sin x\cos x$

$\sec^2x$

$2\cos x+\cot x$

Correct answer:

$\sec^2x$

Explanation:

Whenever you see a trigonometric function squared, start looking for a Pythagorean identity.

The two identities used in this problem are $\sin^2 x + \cos ^2 x=1$ and $\tan^2 x +1 =\sec^2 x$ .

Substitute and solve.

$\sin^2x+\cos^2x+\tan^2x=?$

$(\sin^2x+\cos^2x)+\tan^2x=?$

$(1)+\tan^2x=\sec^2 x$

Report an Error

Example Question #1 : Using Identities Of Squared Functions

Factor and simplify 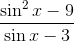$\frac{\sin^2x-9}{\sin x-3}$ .

Possible Answers:

$\sin x \cos x$

$\csc x$

$\cos^2 x+3$

This is already it's most reduced form.

$\sin x+3$

Correct answer:

$\sin x+3$

Explanation:

To reduce 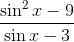$\frac{\sin^2x-9}{\sin x-3}$ , factor the numerator: $\frac{(\sin x-3)(\sin x+3)}{\sin x-3}$

Notice that we can cancel out a $\sin x -3$ .

This leaves us with 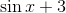$\sin x +3$ .

Report an Error

Example Question #1 : Using Sum And Product Identities

Simplify $\sin x\cot x$ .

Possible Answers:

$\tan x$

$cos \, x$

$\sin x \cos x$

$\cos^2x$

$\csc x$

Correct answer:

$cos \, x$

Explanation:

To simplify $\sin x\cot x$ , break them into their SOHCAHTOA parts:

$\frac{\text{opposite}}{\text{hypotenuse}}*\frac{\text{adjacent}}{\text{opposite}}$ .

Notice that the opposite's cancel out, leaving $\frac{\text{adjacent}}{\text{hypotenuse}}=\cos x$ .

Report an Error

Example Question #2 : Using Sum And Product Identities

Simplify $\csc x \tan x$ .

Possible Answers:

$\cos x$

This is the most simplified version.

$\sin x \cos x$

$\sec x$

Correct answer:

$\sec x$

Explanation:

Break down $\csc x \tan x$ into SOHCAHTOA to solve:

$\csc=\frac{\text{hypotenuse}}{\text{opposite}}$ and $\tan=\frac{\text{opposite}}{\text{adjacent}}$ .

Therefore, $\csc x \tan x=\frac{\text{hypotenuse}}{\text{opposite}}*\frac{\text{opposite}}{\text{adjacent}}$ . Note that the opposite's cancel out, leaving $\frac{\text{hypotenuse}}{\text{adjacent}}$ , which is the same as $\sec x$ .

Report an Error

Example Question #121 : Trigonometry

$\textup{Which of the following expressions is equal to }\frac{\tan \theta }{\sec \theta }\:\textup{?}$

Possible Answers:

$\cos\theta$

$\sin\theta$

$\frac{1}{\cos ^{2}\theta }$

$\csc\theta$

$\cot\theta$

Correct answer:

$\sin\theta$

Explanation:

$\textup{Use identities to solve: }\tan\theta=\frac{\sin \theta }{\cos \theta }\:\:\:\:\:\sec\theta=\frac{1}{\cos \theta }$

$\frac{\tan \theta }{\sec \theta }=\frac{\sin \theta }{\cos \theta }\times\frac{\cos \theta }{1}=\sin\theta$

Report an Error

Example Question #1 : Cones

What is the volume of a cone with a height of and a base with a radius of ?

Possible Answers:

$1521\pi$

$117\pi$

$507\pi$

$396\pi$

Correct answer:

$507\pi$

Explanation:

To find the volume of a cone we must use the equation $V=\frac{1}{3}(A_{base})(H)$ . In this formula, $A_{base}$ is the area of the circular base of the cone, and is the height of the cone.

We must first solve for the area of the base using r=13 .

The equation for the area of a circle is $A=\pi(r^{2})$ . Using this, we can adjust our formula and plug in the value of our radius.

$V=\frac{1}{3}(A_{base})(H)=\frac{1}{3}(\pi r^2)(H)=\frac{1}{3}(\pi (13)^2)(H)$

13^2=169

$V=\frac{1}{3}(169\pi)(H)$

Now we can plug in our given height, H=9 .

$V=\frac{1}{3}(169\pi)(9)$

Multiply everything out to solve for the volume.

$V=\frac{1}{3}(169\pi)(9)=(169\pi)(3)=507\pi$

The volume of the cone is $507\pi$ .

Report an Error

Example Question #1 : Cones

What is the equation of a circle with a center of (5,15) and a radius of 7?

Possible Answers:

(x-5)^2+(y-15)^2=49

(x-5)^2+(y-15)^2=7

(x-5)^2+(y-15)^2=14

(x+5)^2+(y+15)^2=49

Correct answer:

(x-5)^2+(y-15)^2=49

Explanation:

To find the equation of a circle we must first know the standard form of the equation of a circle which is

The letters and represent the -value and -value of the center of the circle respectively.

In this case is 5 and k is 15 so plugging the values into the equation yields (x-5)^2+(y-15)^2=r^2

We then plug the radius into the equation to get (x-5)^2+(y-15)^2=7^2

Square it to yield (x-5)^2+(y-15)^2=49

The equation with a center of (5,15) and a radius of 7 is (x-5)^2+(y-15)^2=49 .

Report an Error

Example Question #2 : Cones

$\textup{Find the volume, to the nearest cubic inch, of a cone with a radius of 8 inches}$

$\textup{at its base and a height of one foot.}$

Possible Answers:

2413

804

1206

302

Correct answer:

804

Explanation:

$V= \frac{1}{3} \pi r^{2}h\;\;\textup{Given: }r=8\textup{ inches}, h=12\textup{ inches}$

$V = \frac{1}{3} \pi\times8^{2}\times12\;\;\;\;\;V = 256\pi\;\;\;V=804.2$

Report an Error

Example Question #1 : Solid Geometry

What is the volume of a cone that has a radius of 3 and a height of 4?

Possible Answers:

$4\pi$

$12\pi$

$36\pi$

$9\pi$

$12\pi$

Correct answer:

$12\pi$

Explanation:

The standard equation for the volume of a cone is

$v=\frac{1}{3}\pi (r)^2h$

where denotes the radius and denotes the height.

Plug in the given values for and to find the answer:

$v=\frac{1}{3}\pi (3)^2(4)=\frac{1}{3}\pi (9)(4)=12\pi$

Report an Error

Example Question #3 : Solid Geometry

Find the volume of the following cone.

Cone

Possible Answers:

$115 \pi m^3$

$130 \pi m^3$

$70 \pi m^3$

$100 \pi m^3$

$85 \pi m^3$

Correct answer:

$100 \pi m^3$

Explanation:

The formula for the volume of a cone is:

$V= \frac{\pi r^{2}h}{3}$

where is the radius of the cone and is the height of the cone.

In order to find the height of the cone, use the Pythagorean Theorem:

A^2 + B^2 = C^2

A^2 + (5m)^2 = (13m)^2

A^2 = 144m^2

A = 12m

Plugging in our values, we get:

$V= \frac{\pi (5m)^2 (12m)}{3}$

$V= \pi (25m^2)(4m)=100 \pi m^3$

Report an Error

View Tutors

Noorulain
Certified Tutor

Daytona State College, Masters in Business Administration, Finance.

View Tutors

Maria
Certified Tutor

University of South Florida-Main Campus, Bachelor of Science, Finance.

View Tutors

Ella
Certified Tutor

University of Houston, Bachelors, Journalism. University of Houston, Juris Doctor, Prelaw Studies.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Dallas Fort Worth, French Tutors in Boston, Algebra Tutors in Atlanta, LSAT Tutors in San Diego, French Tutors in Phoenix, Physics Tutors in Houston, Statistics Tutors in Los Angeles, Reading Tutors in Los Angeles, Computer Science Tutors in New York City, Spanish Tutors in Washington DC

Popular Courses & Classes

MCAT Courses & Classes in Washington DC, SAT Courses & Classes in Miami, GRE Courses & Classes in Washington DC, SSAT Courses & Classes in Miami, MCAT Courses & Classes in Phoenix, Spanish Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Atlanta, MCAT Courses & Classes in Boston, ACT Courses & Classes in Washington DC

Popular Test Prep

ACT Test Prep in Seattle, ACT Test Prep in Washington DC, GRE Test Prep in Houston, MCAT Test Prep in Washington DC, GMAT Test Prep in Houston, ISEE Test Prep in Philadelphia, ISEE Test Prep in Atlanta, ACT Test Prep in San Diego, GMAT Test Prep in Atlanta, LSAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Using Pythagorean Identities

Example Question #1 : Using Identities Of Squared Functions

Example Question #1 : Using Sum And Product Identities

Example Question #2 : Using Sum And Product Identities

Example Question #121 : Trigonometry

Example Question #1 : Cones

Example Question #1 : Cones

Example Question #2 : Cones

Example Question #1 : Solid Geometry

Example Question #3 : Solid Geometry

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: