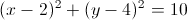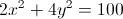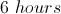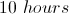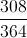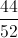Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Equation Of A Circle

The center of a circle is (2, 4) and its radius is . Which of the following could be the equation of the circle?

Possible Answers:

$(x - 2)^{2} + (y - 4)^{2} = 100$

$(x - 2)^{2} + (y - 4)^{2} = 10$

$(x + 2)^{2} + (y + 4)^{2} = 100$

$x^{2} + y^{2} = 100$

$2x^{2} + 4y^{2} = 100$

Correct answer:

$(x - 2)^{2} + (y - 4)^{2} = 100$

Explanation:

The general equation of a circle is $(x - h)^{2} + (y - k)^{2} = r^{2}$ , where the center of the circle is (h, k) and the radius is .

Thus, we plug the values given into the above equation to get $(x - 2)^{2} + (y - 4)^{2} = 100$ .

Report an Error

Example Question #1 : How To Find The Equation Of A Circle

Which one of these equations accurately describes a circle with a center of (2,3) and a radius of ?

Possible Answers:

(x-3)^2+(y-2)^2=25

(x-2)^2+(y-3)^2-25=0

(x^2+4)-(y^2+9)=25

$\sqrt{x^2+y^2-3^2-2^2}=5$

x^2+y^2=25

Correct answer:

(x-2)^2+(y-3)^2-25=0

Explanation:

The standard formula for a circle is (x-a)^2+(y-b)^2=r^2 , with (a,b) the center of the circle and the radius.

Plug in our given information.

(x-a)^2+(y-b^2)=r^2

(x-2)^2+(y-3)^2=25

This describes what we are looking for. This equation is not one of the answer choices, however, so subtract from both sides.

(x-2)^2+(y-3)^2-25=0

Report an Error

Example Question #1 : Equations

Tom is painting a fence 100 feet long. He starts at the West end of the fence and paints at a rate of feet per hour. After hours, Huck joins Tom and begins painting from the East end of the fence at a rate of feet per hour. After hours of the two boys painting at the same time, Tom leaves Huck to finish the job by himself.

If Huck completes painting the entire fence after Tom leaves, how many more hours will Huck work than Tom?

Possible Answers:

$4\ hours$

$3\ hours$

$6\ hours$

$5\ hours$

$10\ hours$

Correct answer:

$6\ hours$

Explanation:

Tom paints for a total of hours (2 on his own, 2 with Huck's help). Since he paints at a rate of feet per hour, use the formula

$distance = rate \times time$ (or d = rt )

to determine the total length of the fence Tom paints.

d = (5)(4)

d = 20 feet

Subtracting this from the total length of the fence 100 feet gives the length of the fence Tom will NOT paint: 100 - 20 = 80 feet. If Huck finishes the job, he will paint that feet of the fence. Using d = rt , we can determine how long this will take Huck to do:

80 = 8(t)

t = 10 hours.

If Huck works hours and Tom works hours, he works more hours than Tom.

Report an Error

Example Question #1 : Equations

Simplify the fraction to the lowest terms:

$\frac{924}{1092}$

Possible Answers:

$\frac{308}{364}$

Cannot be simplified

$\frac{11}{13}$

$\frac{44}{52}$

Correct answer:

$\frac{11}{13}$

Explanation:

Find the common multiple between the numerator and denominator.

$\frac{924}{1092}$

divide numerator and denominator by 3:

$\frac{308}{364}$

divide numerator and denominator by 7:

$\frac{44}{52}$

divide numerator and denominator by 4:

$\frac{11}{13}$

Cannot be divided any more- lowest terms.

Report an Error

Example Question #1 : Equations

Solve the following equation for x in terms of the other variables:

$\frac{ax}{b-ax}=2$

Possible Answers:

$x=\frac{2b}{3a}$

$x=\frac{3a}{2b}$

$x=\frac{2a}{3b}$

3ax=2b

$x=\frac{3b}{2a}$

Correct answer:

$x=\frac{2b}{3a}$

Explanation:

$\frac{ax}{b-ax}=2$

Multiply both sides by (b-ax) to get:

ax=2(b-ax)

Distribute the :

ax=2b-2ax

Combine like terms:

3ax=2b

Divide both sides by :

$x=\frac{2b}{3a}$

Report an Error

Example Question #2 : Equations

Solve the following equation for x in terms of the other variables:

bcx=a

Possible Answers:

$x=\frac{ab}{c}$

$x=\frac{c}{ab}$

$x=\frac{a}{bc}$

$x=\frac{bc}{a}$

$x=\frac{b}{c}$

Correct answer:

$x=\frac{a}{bc}$

Explanation:

bcx=a

Divide both sides by :

$x=\frac{a}{bc}$

Report an Error

Example Question #1 : Equations

If given the equation 8x + 2x -5 , with a positive integer, the result must be an integer multiple of:

Possible Answers:

Correct answer:

Explanation:

The mathematical expression given in the question is 8x + 2x -5 . Adding together like terms, 8x + 2x , this can be simplified to 10x -5 . The expression 10x -5 can be factored as 5(2x -1) . For every positive integer , must be a multiple of 5. If x=1 , then 5(2x - 1) = 5 , which is not an integer multiple of 2, 8, 10, or 15. Therefore, the correct answer is 5.

Report an Error

Example Question #1 : Equations

Cindy's Cotton Candy sells cotton candy by the bag. Her monthly fixed costs are $\$150$ . It costs $\$2.50$ to make each bag and she sells them for $\$4.00$ .

What is the monthly break-even point?

Possible Answers:

$225\; bags$

$150\; bags$

$80\; bags$

$60\; bags$

$100\; bags$

Correct answer:

$100\; bags$

Explanation:

Costs=150+2.50x

Revenues = 4.00x

The break-even point occurs when the costs=revenues .

The equation to solve becomes

4x=150+2.5x so the break-even point is $100 \; bags$ .

Report an Error

Example Question #1 : Equations

Cindy's Cotton Candy sells cotton candy by the bag. Her monthly fixed costs are $\$150$ . It costs $\$2.50$ to make each bag and she sells them for $\$4.00$ .

To make a profit of $\$150$ , how many bags of cotton candy must be sold?

Possible Answers:

$250\; bags$

$200\; bags$

$150\; bags$

$100\; bags$

$300\; bags$

Correct answer:

$200\; bags$

Explanation:

Costs=150+2.50x

Revenues = 4.00x

Profits = Revenues - Costs = 4x - (150+2.5x)=1.5x -150

So the equation to solve becomes 150 = 1.5x - 150 , or $x=200\; bags$ must be sold to make a profit of $\$150$ .

Report an Error

Example Question #3 : Equations

Solve for and to satisfy both equations in the system:

$\begin{Bmatrix} 6x+y = 25 \\ 2x-3y = 25 \end{Bmatrix}$

Possible Answers:

x = 3 , y = 7

x = -5 , y = 5

x=5 , y = 5

x= -5 , y = -5

x = 5 , y= -5

Correct answer:

x = 5 , y= -5

Explanation:

The two equations in this system can be combined by addition or subtraction to solve for and . Isolate the variable to solve for it by multiplying the top equation by so that when the equations are combined the term disappears.

$3\times(6x + y = 25)$

$\rightarrow 18x+3y = 75$

$\rightarrow (18x +3y = 75) + (2x - 3y = 25)$

$\rightarrow 20x = 100$

Divide both sides by to find as the value for .

Substituting for in both of the two equations in the system and solving for gives a value of for .

Report an Error

View Tutors

Briana
Certified Tutor

University of Miami, Doctor of Philosophy, English.

View Tutors

Chris
Certified Tutor

University of New Mexico-Main Campus, Bachelor in Arts, Music. New Mexico Highlands University, Master's/Graduate, ATCP K-8.

View Tutors

Walter
Certified Tutor

Schoolcraft College, Associate in Science, Computer Programming, General. Western Governors University, Bachelor of Science, ...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Phoenix, Math Tutors in San Francisco-Bay Area, Calculus Tutors in Los Angeles, Biology Tutors in Miami, Physics Tutors in Denver, French Tutors in Dallas Fort Worth, SAT Tutors in Boston, English Tutors in Boston, MCAT Tutors in New York City, GMAT Tutors in Washington DC

Popular Courses & Classes

Spanish Courses & Classes in Los Angeles, ISEE Courses & Classes in Chicago, GMAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in New York City, ISEE Courses & Classes in Boston, ACT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Houston, ACT Courses & Classes in Phoenix, MCAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Dallas Fort Worth

Popular Test Prep

SSAT Test Prep in Dallas Fort Worth, SSAT Test Prep in New York City, ACT Test Prep in Chicago, GRE Test Prep in New York City, GMAT Test Prep in Boston, ACT Test Prep in Phoenix, ACT Test Prep in Dallas Fort Worth, SSAT Test Prep in Denver, GMAT Test Prep in Denver, ISEE Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : How To Find The Equation Of A Circle

Example Question #1 : How To Find The Equation Of A Circle

Example Question #1 : Equations

Example Question #1 : Equations

Example Question #1 : Equations

Example Question #2 : Equations

Example Question #1 : Equations

Example Question #1 : Equations

Example Question #1 : Equations

Example Question #3 : Equations

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: