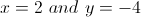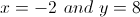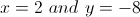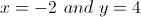We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #27 : Equations

An art show wants to focus on sculpture but will also accept paintings and drawings. The show has room for 140 pieces and will display them in a ratio of scupltures to painting to drawings. How many sculptures will be displayed?

Possible Answers:

Correct answer:

Explanation:

Since the paintings and the drawings have the same ratio, they will have the same number on display.

Let number of paintings displayed = number of drawings displayed.

Then, 140 - 2x = number of sculptures displayed.

Set up a proportion:

$\frac{sculptures}{drawings}=\frac{140 - 2x}{x}=\frac{3}{2}$

Solve by cross multiplying to get 2(140-2x)=3x or 280 - 4x = 3x .

Then add to both sides to get 280 = 7x .

Then divide by to get x=40 .

So there are drawings and paintings in the show, leaving the last spots for sculptures.

Report an Error

Example Question #1511 : High School Math

What number is $125\%$ of 240 ?

Possible Answers:

300

340

325

285

365

Correct answer:

300

Explanation:

Verbal cues include "IS" means equal and "OF" means multiplication.

So the equation to solve becomes $n=1.25\cdot 240=300$

Report an Error

Example Question #221 : Algebra Ii

is what percent of ?

Possible Answers:

Correct answer:

Explanation:

Verbal cues include "IS" means equals and "OF" means multiplication.

So the equation to solve becomes

$15=P\cdot 75$ and dividing both sides by gives $P=0.20 \; or \; 20\%$

Report an Error

Example Question #1 : Systems Of Equations

Solve the system of equations.

4x+y=16

2x+3y=18

Possible Answers:

(-3,4)

(-4,3)

(3,4)

None of the other answers are correct.

(4,3)

Correct answer:

(3,4)

Explanation:

Isolate in the first equation.

y=16-4x

Plug into the second equation to solve for .

2x+3(16-4x)=18

2x+48-12x=18

-10x+48=30

-10x=-30

x=3

Plug into the first equation to solve for .

4(3)+y=16

12+y=16

y=4

Now we have both the and values and can express them as a point: (3,4) .

Report an Error

Example Question #1 : Linear Systems With Two Variables

Solve for and .

3x+2y=2

2x+2y=4

Possible Answers:

Cannot be determined.

$x=-2\ and\ y=4$

$x=-2\ and\ y=8$

$x=2\ and\ y=-8$

$x=2\ and\ y=-4$

Correct answer:

$x=-2\ and\ y=4$

Explanation:

1st equation: 3x+2y=2

2nd equation: 2x+2y=4

Subtract the 2nd equation from the 1st equation to eliminate the "2y" from both equations and get an answer for x:

Plug the value of into either equation and solve for :

2(-2)+2y=4

-4+2y=4

2y=4+4

2y=8

Report an Error

Example Question #33 : Equations

Solve for :

$\left | 5x + 39 \right | = 44$

Possible Answers:

$x = -16\frac{3}{5} \textrm{ or }x = 16\frac{3}{5}$

$x = -16\frac{3}{5} \textrm{ or } x = 1$

$x = 16\frac{3}{5}$

$x = 1 \textrm{ or }x = 16\frac{3}{5}$

$x = -1 \textrm{ or } x = 1$

Correct answer:

$x = -16\frac{3}{5} \textrm{ or } x = 1$

Explanation:

Rewrite $\left | 5x + 39 \right | = 44$ as a compound statement and solve each part separately:

$\left | 5x + 39 \right | = 44$

$5x + 39 = - 44 \textrm{ or }5x + 39 = 44$

5x + 39 = - 44

5x + 39 - 39 = - 44- 39

5x = - 83

$5x \div 5 = - 83 \div 5$

$x = -16\frac{3}{5}$

5x + 39 = 44

5x + 39 - 39 = 44- 39

5x = 5

$5x \div 5 =5 \div 5$

x = 1

Therefore the solution set is $\left \{-16\frac{3}{5}, 1 \right \}$ .

Report an Error

Example Question #34 : Equations

Solve the following equation for :

3(x+2) = 4(x-3)

Possible Answers:

x = 2

x = -18

x = 18

x = -9

x = -6

Correct answer:

x = 18

Explanation:

3(x+2) = 4(x-3)

The first step in solving this equation is to distribute the 3 and the 4 through the parentheses:

$3\cdot x+3\cdot2 = 4\cdot x-4\cdot 3$

Simplify:

3x+6 = 4x-12

Now, we want to get like terms on the same sides of the equation. That is, all of the terms with an should be on one side, and those without an should be on the other. To do this, we first subtract from both sides:

3x+6 -4x= 4x-12-4x

Simplify:

-x+6 = -12

Now, we subtract 6 from both sides:

-x+6-6 = -12-6

-x = -18

x = 18

Report an Error

Example Question #31 : Equations

Goldenrod paint is made by mixing one part red with three parts yellow. How many gallons of yellow paint should be mixed with two quarts of red paint?

Possible Answers:

$1.25\; gallons$

$1.00\; gallon$

$1.75\; gallons$

$1.50\; gallons$

$0.75\; gallons$

Correct answer:

$1.50\; gallons$

Explanation:

This problem is solved using proportions and the following conversion factor:

$4\; quarts=1\; gallon$

Let yellow quarts of paint.

$\frac{red}{yellow}=\frac{1}{3}=\frac{2\; quarts}{x\; quarts}$

Then cross multiply to get $x=6\; quarts = 1.50 \; gallons$ .

Report an Error

Example Question #32 : Equations

Solve for :

$\frac{1}{2}(x+3)=\frac{1}{3}(x+5)$

Possible Answers:

Correct answer:

Explanation:

Multiply both sides by to eliminate the fractions to get 3(x+3)=2(x+5) .

Then use the distributive property to get 3x+9=2x+10 .

Now subtract from both sides to get x+9=10 .

Now subtract from both sides to get x=1 .

Report an Error

Example Question #33 : Equations

To mail a package, there is an initial charge of $55\cent$ to cover the first ounce, with another $25\cent$ for each additional ounce. How much does it cost to mail a half pound package?

Possible Answers:

$\$ 3.50$

$\$ 2.00$

$\$ 4.40$

$\$ 2.30$

$\$ 3.95$

Correct answer:

$\$ 2.30$

Explanation:

$1\; pound = 16 \; ounces$ , so we are trying to mail ounces. The total postage becomes $0.55+7(0.25)=0.55+1.75=\$ 2.30$ .

Report an Error

View Tutors

Luz
Certified Tutor

Arizona State University, Bachelor in Arts, English.

View Tutors

Smriti
Certified Tutor

New Jersey Institute of Technology, Bachelor of Science, Human-Computer Interaction.

View Tutors

Stephen
Certified Tutor

SUNY at Albany, Bachelor in Arts, Spanish. SUNY at Albany, Bachelor in Arts, Russian.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Atlanta, Biology Tutors in Philadelphia, ISEE Tutors in Boston, Biology Tutors in Houston, Spanish Tutors in Atlanta, Algebra Tutors in Miami, Math Tutors in Chicago, Reading Tutors in Washington DC, ISEE Tutors in Dallas Fort Worth, Statistics Tutors in Houston

Popular Courses & Classes

ACT Courses & Classes in San Diego, GMAT Courses & Classes in Miami, Spanish Courses & Classes in Houston, LSAT Courses & Classes in Miami, ISEE Courses & Classes in Boston, GMAT Courses & Classes in Los Angeles, ACT Courses & Classes in Boston, LSAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Washington DC, SSAT Courses & Classes in Miami

Popular Test Prep

GMAT Test Prep in Los Angeles, ACT Test Prep in New York City, ACT Test Prep in Boston, SAT Test Prep in Los Angeles, SAT Test Prep in New York City, ISEE Test Prep in Washington DC, MCAT Test Prep in Washington DC, SSAT Test Prep in Dallas Fort Worth, SAT Test Prep in Seattle, ACT Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #27 : Equations

Example Question #1511 : High School Math

Example Question #221 : Algebra Ii

Example Question #1 : Systems Of Equations

Example Question #1 : Linear Systems With Two Variables

Example Question #33 : Equations

Example Question #34 : Equations

Example Question #31 : Equations

Example Question #32 : Equations

Example Question #33 : Equations

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: