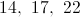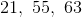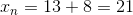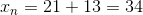We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Multiplying And Dividing Factorials

Find the value of:

$\frac{7!}{3!}$

Possible Answers:

840

210

2.33

2520

Correct answer:

840

Explanation:

The factorial sign (!) just tells us to multiply that number by every integer that leads up to it. So, $\frac{7!}{3!}$ can also be written as:

$\frac{(7\times6\times5\times4\times3\times2\times1)}{(3\times2\times1)}$

To make this easier for ourselves, we can cancel out the numbers that appear on both the top and bottom:

$7\times6\times5\times4 = 840$

Report an Error

Example Question #1 : Multiplying And Dividing Factorials

Solve the following expression.

$\frac{10!}{8!}$

Possible Answers:

720

1.25

Correct answer:

Explanation:

$\frac{10!}{8!}=\frac{10*9*8*7*6*5*4*3*2*1}{8*7*6*5*4*3*2*1}$

This expression can be simplified because all terms in the expression for 8! are also found in the expression for 10!. By writing the expression below, we are able to cancel 8!.

$\frac{10*9*8!}{8!}=10*9=90$

Report an Error

Example Question #2 : Multiplying And Dividing Factorials

Solve:

$\frac{10!}{7!}$

Possible Answers:

100

720

800

640

Correct answer:

720

Explanation:

Both the numerator and denominator are factorials. If you expanded both, everything would cancel out except for $10\cdot9\cdot8$ in the numerator. Multiply those together to get 720.

Report an Error

Example Question #1 : Multiplying And Dividing Factorials

Simplify $\frac{ 8!}{6!}$ .

Possible Answers:

Correct answer:

Explanation:

8! = 8*7*6*5* . . . *2*1

6! = 6*5*4*3*2*1

Thus, $\frac{8!}{6!} = 8*7$ since the remaining terms cancel out. 56 is the simplified result.

Report an Error

Example Question #1 : Factorials

Stewie has $\frac{5!}{3!}$ marbles in a bag. How many marbles does Stewie have?

Possible Answers:

1.66

Correct answer:

Explanation:

5!/3! = (5*4*3*2*1)/(3*2*1)

Simplifying this equation we notice that the 3's, 2's, and 1's cancel so

5!/3! = 5*4 = 20

Alternative Solution

5!/3! = (120/6) = 20

Report an Error

Example Question #1 : Multiplying And Dividing Factorials

Which of the following is NOT the same as $\frac{6!\times5!}{4!}$ ?

Possible Answers:

$6\times5!$

$6\times5^{2}\times4!$

$\frac{6\times(5!)^2}{4!}$

$5\times6!$

$30\times5!$

Correct answer:

$6\times5!$

Explanation:

The cancels out all of except for the parts higher than 4, this leaves a 6 and a 5 left to multilpy

Report an Error

Example Question #4 : Multiplying And Dividing Factorials

Simplify and solve $\frac{100!}{97!}$ .

Possible Answers:

9700

970,200

$7.5*10^{15}$

1.03

Correct answer:

970,200

Explanation:

Remember a number followed by a ! is a factorial. A factorial is the product of the given number and all of the numbers smaller than it down to zero. For example, 5!=5*4*3*2*1 .

Rather than do all of the math involved for 100! , notice that $\frac{100!}{97!}$ is the same as $\frac{100*99*98*97!}{97!}$

From here, the 97! 's cancel out, leaving us with 100*99*98=970,200 .

Report an Error

Example Question #151 : Mathematical Relationships And Basic Graphs

Which of the following is equivalent to $6!\times4!$ ?

Possible Answers:

10!

None of the other answers are correct.

$30\times(4!)^2$

$(6!)^{2}-4!$

24!

Correct answer:

$30\times(4!)^2$

Explanation:

This is a factorial question. The formula for factorials is $n! = n\times(n-1)\times(n-2)\times...\times1$ .

$6!=6\times5\times4! = 30\times 4!$

Report an Error

Example Question #1441 : High School Math

Consider the Fibonacci sequence written below. What are the next three terms?

$\small 1,\1,\ 2,\ 3,\ 5,\ 8,\ 13,...$

Possible Answers:

$18, \23,\ 28$

$16,\ 21,\ 24$

$21,\ 34,\ 55$

$21,\ 55,\ 63$

$14,\ 17 ,\ 22$

Correct answer:

$21,\ 34,\ 55$

Explanation:

Each number in the Fibonacci sequence can be calculated by the sum of the previous two numbers.

$x_n=x_{n-1}+x_{n-2}$

The next term in the sequence will be the sum of the two terms preceding it: 8 and 13.

x_n=13+8=21

$\small 1,\1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21...$

The next term will be the sum of 13 and 21.

x_n=21+13=34

$\small 1,\1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34...$

The next term will be the sum of 21 and 34.

x_n=34+21=55

$\small 1,\1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,\ 55...$

Report an Error

Example Question #1 : Summations And Sequences

Which of the following is a geometric sequence?

Possible Answers:

$t_{0}=4$

$t_{n}=t_{n-1}\times 3$

$t_{0}=5$

$t_{n}=t_{n-1}+3$

$t_{0}=2$

$t_{n} = t_{n-1}^{6}$

$t_{0}=4$

$t_{n}=t_{n-1}+3.4$

$t_{0}=10$

$t_{n}=t_{n-1}+5$

Correct answer:

$t_{0}=4$

$t_{n}=t_{n-1}\times 3$

Explanation:

A geometric sequence is one in which the next term is found by mutlplying the previous term by a particular constant. Thus, we look for an implicit definition which involves multiplication of the previous term. The only possibility is:

$t_{0}=4$

$t_{n}=t_{n-1}\times 3$

Report an Error

View Tutors

Marcie
Certified Tutor

University of Georgia, Master of Arts, Mathematics.

View Tutors

Hongqiu
Certified Tutor

University at Buffalo, Bachelor of Science, Public Health.

View Tutors

Carolyn
Certified Tutor

University of California-Los Angeles, Bachelor in Arts, Mathematics.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Chicago, Math Tutors in Boston, Physics Tutors in New York City, Computer Science Tutors in Dallas Fort Worth, Physics Tutors in Atlanta, Reading Tutors in Houston, Computer Science Tutors in Denver, Algebra Tutors in Atlanta, ISEE Tutors in San Diego, Physics Tutors in Phoenix

Popular Courses & Classes

MCAT Courses & Classes in New York City, ISEE Courses & Classes in Phoenix, GMAT Courses & Classes in Phoenix, LSAT Courses & Classes in Houston, GMAT Courses & Classes in Chicago, LSAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Seattle, GRE Courses & Classes in Houston, LSAT Courses & Classes in Miami

Popular Test Prep

MCAT Test Prep in Atlanta, SSAT Test Prep in Philadelphia, LSAT Test Prep in Houston, GRE Test Prep in Chicago, GMAT Test Prep in Chicago, ISEE Test Prep in Chicago, GMAT Test Prep in Phoenix, LSAT Test Prep in Boston, SAT Test Prep in San Diego, GMAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Multiplying And Dividing Factorials

Example Question #1 : Multiplying And Dividing Factorials

Example Question #2 : Multiplying And Dividing Factorials

Example Question #1 : Multiplying And Dividing Factorials

Example Question #1 : Factorials

Example Question #1 : Multiplying And Dividing Factorials

Example Question #4 : Multiplying And Dividing Factorials

Example Question #151 : Mathematical Relationships And Basic Graphs

Example Question #1441 : High School Math

Example Question #1 : Summations And Sequences

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: