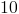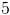We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Graphing Exponential Functions

Find the -intercept(s) of $y=\frac{x^2+9x+8}{x^2-44}$ .

Possible Answers:

x=-1 and x=-8

x=1 and x=8

$x=\frac{1}{8}$

$x=2\sqrt{2}$

$x=2\sqrt{11}$

Correct answer:

x=-1 and x=-8

Explanation:

To find the -intercept(s) of $y=\frac{x^2+9x+8}{x^2-44}$ , we need to set the numerator equal to zero and solve.

First, notice that x^2+9x+8 can be factored into (x+1)(x+8) . Now set that equal to zero: 0=(x+1)(x+8) .

Since we have two sets in parentheses, there are two separate values that can cause our equation to equal zero: one where x+1=0 and one where x+8=0 .

Solve for each value:

x+1=0

x=-1

and

x+8=0

x=-8 .

Therefore there are two -interecpts: x=-1 and x=-8 .

Report an Error

Example Question #4 : Graphing Exponential Functions

Find the -intercept(s) of $y=\frac{x^3+2x+8}{x^2-36}$ .

Possible Answers:

x=6 or x=-6

x=0

The function does not cross the -axis.

x=-1.67

x=1

Correct answer:

x=-1.67

Explanation:

To find the -intercept(s) of $y=\frac{x^3+2x+8}{x^2-36}$ , we need to set the numerator equal to zero.

That means 0=x^3+2x+8 .

The best way to solve for a funky equation like this is to graph it in your calculator and calculate the roots. The result is $x\approx -1.67$ .

Report an Error

Example Question #1 : Algebra I

What would be the midpoint of a line segment with endpoints at (0,1) and (5,7) ?

Possible Answers:

(1,1)

$(\frac{5}{2},\frac{9}{2})$

$(\frac{5}{2},\frac{5}{2})$

$(\frac{5}{2},4)$

(5,6)

Correct answer:

$(\frac{5}{2},4)$

Explanation:

The midpoint of a line segment is halfway between the two $\small x$ values and halfway between the two $\small y$ values.

Mathematically, that would be the average of each coordinate: $(\frac{x_2+x_1}{2},\frac{y_2+y_1}{2})$ .

Plug in the (x,y) values from the given points and solve.

$(\frac{5+0}{2},\frac{7+1}{2})$

$(\frac{5}{2},\frac{8}{2})$

We can simplify the fraction to give our final answer.

$(\frac{5}{2},4)$

Report an Error

Example Question #2 : Algebra I

What would be the midpoint of a line segment with endpoints at (1,6) and (9,9) ?

Possible Answers:

(4.5,4.5)

(5,7)

(5,7.5)

(0,0)

(2.5,7.5)

Correct answer:

(5,7.5)

Explanation:

The midpoint of a line segment is halfway between the two $\small x$ values and halfway between the two $\small y$ values.

Mathematically, that would be the average of each coordinate: $(\frac{x_2+x_1}{2},\frac{y_2+y_1}{2})$ .

Plug in the (x,y) values from the given points and solve.

$(\frac{9+1}{2},\frac{9+6}{2})$

$(\frac{10}{2},\frac{15}{2})$

Simplify the fractions to get the final answer.

(5,7.5)

Report an Error

Example Question #3 : Midpoint And Distance Formulas

If a line has a midpoint at (2,5) , and the endpoints are (0,0) and (4,y) , what is the value of ?

Possible Answers:

2.5

Correct answer:

Explanation:

The midpoint of a line segment is halfway between the two $\small x$ values and halfway between the two $\small y$ values.

Mathematically, that would be the average of the coordinates: $(\frac{x_2+x_1}{2},\frac{y_2+y_1}{2})$ .

Plug in the (x,y) values from the given points.

$(\frac{4+0}{2},\frac{y+0}{2})=(2,5)$

Now we can solve for the missing value.

$(\frac{4}{2},\frac{y}{2})=(2,5)$

$\frac{4}{2}=2$

The $\small x$ values reduce, so both $\small x$ values equal $\small 2$ . Now we need to create a new equation to solve for the $\small y$ value.

$\frac{y}{2}=5$

Multiply both sides by to solve.

$(2)\frac{y}{2}=5(2)$

y=10

Report an Error

Example Question #3 : Algebra I

What is the midpoint of a line segment with endpoints (1,1) and (12,12) ?

Possible Answers:

(6,6)

$(\frac{1}{2},\frac{3}{4})$

$(\frac{13}{2},\frac{13}{2})$

(13,13)

(11,-11)

Correct answer:

$(\frac{13}{2},\frac{13}{2})$

Explanation:

The midpoint formula is this: $(\frac{x_2+x_1}{2},\frac{y_2+y_1}{2})$ .

Plug in the given values from our points and solve:

$(\frac{x_2+x_1}{2},\frac{y_2+y_1}{2})$

$(\frac{12+1}{2},\frac{12+1}{2})$

$(\frac{13}{2},\frac{13}{2})$

Report an Error

Example Question #5 : Midpoint And Distance Formulas

What is the midpoint of the line segment with endpoints at (6,3) and (9,2) ?

Possible Answers:

(7,3)

$(\frac{2}{3},\frac{5}{3})$

$(\frac{2}{15},\frac{2}{5})$

$(\frac{9}{2},\frac{5}{2})$

$(\frac{15}{2},\frac{5}{2})$

Correct answer:

$(\frac{15}{2},\frac{5}{2})$

Explanation:

The midpoint formula is this: $(\frac{x_2+x_1}{2},\frac{y_2+y_1}{2})$ .

Plug in the given values from our points and solve:

$(\frac{x_2+x_1}{2},\frac{y_2+y_1}{2})$

$(\frac{9+6}{2},\frac{2+3}{2})$

$(\frac{15}{2},\frac{5}{2})$

Report an Error

Example Question #6 : Midpoint And Distance Formulas

Find the midpoint between (4, 3) and (6, 9).

Possible Answers:

$\left ( 5,6 \right )$

$\left ( 3,6 \right )$

$\left ( 0,6 \right )$

$\left ( 6,5 \right )$

$\left ( -5,6 \right )$

Correct answer:

$\left ( 5,6 \right )$

Explanation:

Add up the 's and divide in half, which results in 5. Do the same to the 's and you get 6. Put the and in an ordered pair so that your answer is (5, 6).

Report an Error

Example Question #4 : Algebra I

What is the midpoint of the line segment which connects (-6, 8) and (2, 12) ?

Possible Answers:

(2, 10)

(-8, -4)

(-4, 20)

(-2, 10)

(8, 4)

Correct answer:

(-2, 10)

Explanation:

To find the midpoint of a line segment, we find the average of the x and y coordinates of the endpoints. The average of two numbers is the sum of those numbers divided by . Thus, to find the x-coordinate of our midpoint, we find the average of and , and we get (-6+2)/2=-4/2 = -2 .

To find the y-coordinate of our midpoint, we find the average of and , which is (8+12)/2=20/2 = 10 .

Thus, our midpoint is (-2, 10).

Report an Error

Example Question #8 : Midpoint And Distance Formulas

Find the midpoint of the line segment with end points (-2,3) and (-4,16) .

Possible Answers:

(3,-9.5)

(-3,9.5)

(3,9.5)

(-6,19)

(6,-19)

Correct answer:

(-3,9.5)

Explanation:

To find the midpoint of a line segment, use the standard equation:

$(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})$

Plugging in the given points:

$(\frac{-2+-4}{2},\frac{3+16}{2})=(-3,9.5)$

Report an Error

View Tutors

Deb
Certified Tutor

Salisbury University, Bachelors, Secondary Mathematics Education . Salisbury University, Masters, Education in Secondary Math...

View Tutors

Joseph
Certified Tutor

Bank Street College of Education , Master's/Graduate, Early Childhood and Childhood General Education.

View Tutors

Jamila
Certified Tutor

Lamar University, Bachelor in Arts, General Studies.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Atlanta, SSAT Tutors in Phoenix, Reading Tutors in Phoenix, MCAT Tutors in Dallas Fort Worth, Biology Tutors in Dallas Fort Worth, Reading Tutors in Los Angeles, GMAT Tutors in Seattle, Physics Tutors in Dallas Fort Worth, Spanish Tutors in Atlanta, French Tutors in Phoenix

Popular Courses & Classes

SSAT Courses & Classes in Chicago, ACT Courses & Classes in Los Angeles, MCAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Houston, SSAT Courses & Classes in San Diego, SSAT Courses & Classes in Phoenix, GRE Courses & Classes in San Diego, ISEE Courses & Classes in New York City, LSAT Courses & Classes in Houston, Spanish Courses & Classes in Los Angeles

Popular Test Prep

LSAT Test Prep in Atlanta, GRE Test Prep in Atlanta, MCAT Test Prep in Phoenix, GRE Test Prep in Chicago, LSAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Washington DC, ACT Test Prep in Los Angeles, SAT Test Prep in Los Angeles, ISEE Test Prep in Denver, SAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #2 : Graphing Exponential Functions

Example Question #4 : Graphing Exponential Functions

Example Question #1 : Algebra I

Example Question #2 : Algebra I

Example Question #3 : Midpoint And Distance Formulas

Example Question #3 : Algebra I

Example Question #5 : Midpoint And Distance Formulas

Example Question #6 : Midpoint And Distance Formulas

Example Question #4 : Algebra I

Example Question #8 : Midpoint And Distance Formulas

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: