All High School Math Resources
Example Questions
Example Question #1041 : High School Math
What is 
When adding polynomials you add the integers in front of like-termed variables raised to the same power.
So in this case we take the numbers and add
After addition we add the variable 
We have the answer 
Example Question #575 : Pre Algebra
What is 
When subtracting polynomials you only subtract the integers in front of like-termed variables raised to the same power.
So in this case we take the numbers and subtract them
After subtraction we add the variable to get

The answer is 
Example Question #1041 : High School Math
Simplify
When adding variables raised to the same power, add the values in front of the like-termed variables. In this case, we add 


Example Question #1042 : High School Math
Simplify
When dividing variables raised to the same power, subtract the power of the bottom term from the power of the top term. In this case, subtract 


Example Question #1 : Equilateral Triangles
You are given that the perimeter of an equilateral triangle is 






By definition, an equilateral triangle has three congruent sides. The perimeter is the sum of those sides. Thus, to find the length of just one of those sides, we can divide the perimeter of the triangle by three.



Example Question #1 : How To Find The Area Of An Equilateral Triangle
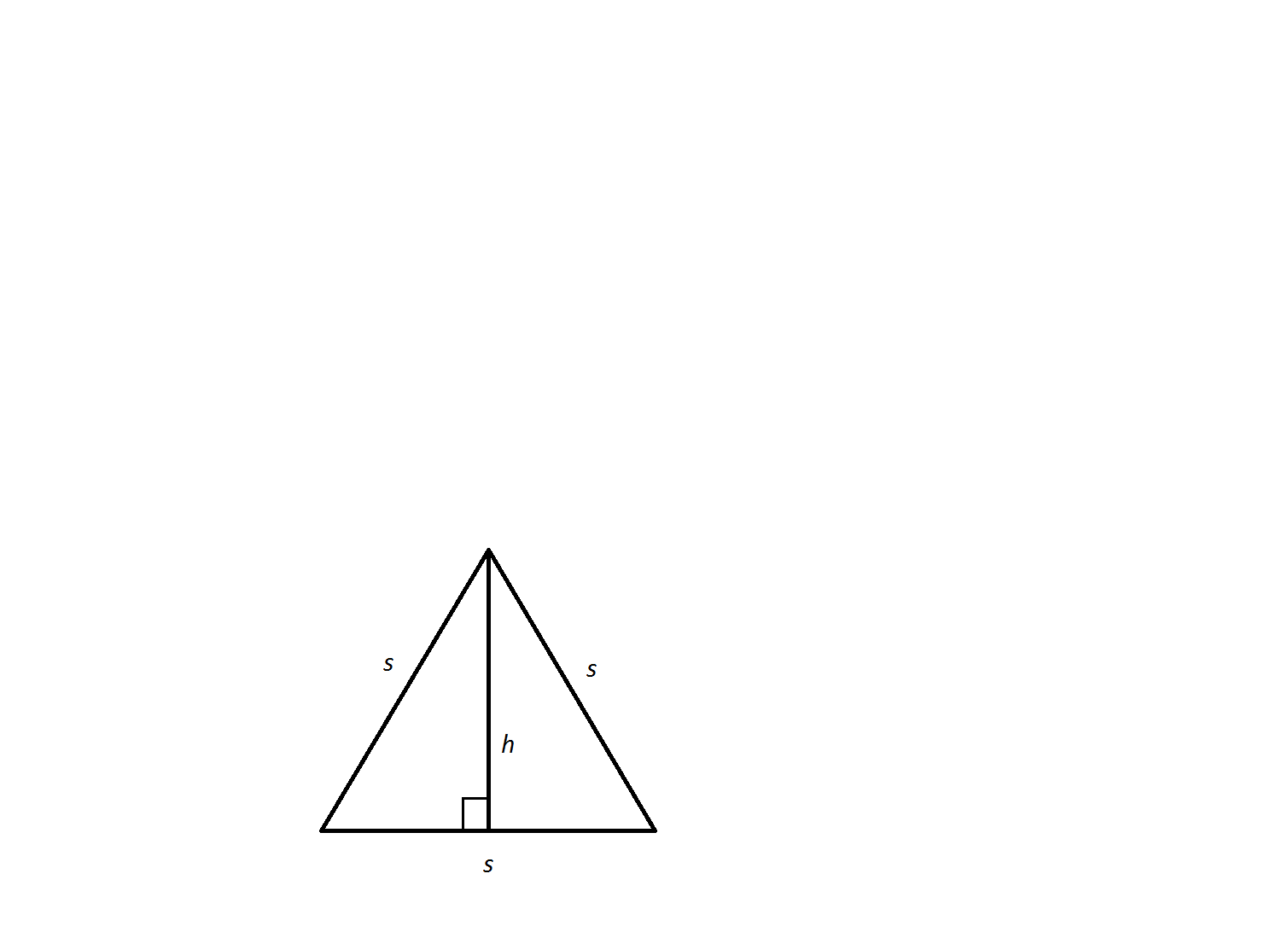
An equilateral triangle has a side length of 
Not enough information to solve
The area of an equilateral triangle is found using the following formula.

Example Question #1 : Equilateral Triangles
The area of square ABCD is 50% greater than the perimeter of the equilateral triangle EFG. If the area of square ABCD is equal to 45, then what is the area of EFG?
50√3
25√3
50
25
30
25√3
If the area of ABCD is equal to 45, then the perimeter of EFG is equal to x * 1.5 = 45. 45 / 1.5 = 30, so the perimeter of EFG is equal to 30. This means that each side is equal to 10.
The height of the equilateral triangle EFG creates two 30-60-90 triangles, each with a hypotenuse of 10 and a short side equal to 5. We know that the long side of 30-60-90 triangle (here the height of EFG) is equal to √3 times the short side, or 5√3.
We then apply the formula for the area of a triangle, which is 1/2 * b * h. We get 1/2 * 10 * 5√3 = 5 * 5√3 = 25√3.
In general, the height of an equilateral triangle is equal to √3 / 2 times a side of the equilateral triangle. The area of an equilateral triangle is equal to 1/2 * √3s/ 2 * s = √3s2/4.
Example Question #2 : How To Find The Area Of An Equilateral Triangle
What is the area of an equilateral triangle with sides 12 cm?
12√2
72√3
36√3
18√3
54√2
36√3
An equilateral triangle has three congruent sides and results in three congruent angles. This figure results in two special right triangles back to back: 30° – 60° – 90° giving sides of x - x √3 – 2x in general. The height of the triangle is the x √3 side. So Atriangle = 1/2 bh = 1/2 * 12 * 6√3 = 36√3 cm2.
Example Question #4 : Equilateral Triangles
The length of one side of an equilateral triangle is ten. What is the area of the triangle?
To calculate the height, the length of a perpendicular bisector must be determined. If a perpendicular bisector is drawn in an equilateral triangle, the triangle is divided in half, and each half is a congruent 30-60-90 right triangle. This type of triangle follows the equation below.
The length of the hypotenuse will be one side of the equilateral triangle.

The side of the equilateral triangle that represents the height of the triangle will have a length of 
To calculate the area of the triangle, multiply the base (one side of the equilateral triangle) and the height (the perpendicular bisector) and divide by two.
Example Question #2 : Equilateral Triangles

What is the area of an equilateral triangle with a side length of 
Not enough information to solve
In order to find the area of the triangle, we must first calculate the height of its altitude. An altitude slices an equilateral triangle into two 



Therefore, we can find the height of the altitude of this triangle by designating a value for 



Now, we can calculate the area of the triangle via the formula 
All High School Math Resources
















































