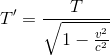We must first determine the amount of time that the ball is in the air, then use the horizontal velocity to solve for the distance travelled.

In order to solve for the amount of time, we need to know the vertical initial velocity of the cannonball. This is given by the equation . Using the initial velocity of  we determine that the vertical initial velocity is 

Knowing this, we can solve the amount of time it will take for the cannon ball to reach its maximum peak, with a velocity of  using the equation 

This is the amount of time it takes for the ball to reach its peak, not the total time it is in the air. Since the ball must drop from the maximum height, we double the time and find that total flight time is 20.8s.

The next step is determining the horizontal initial velocity from the cannon. This is determined using the equation below.

Since we assume that there is no air resistance, we can conclude that the horizontal velocity of the cannonball will remain constant throughout its flight. As a result, the total displacement equation is simplified to the following: .

On earth, .

The law of universal gravitation is equal to .

We can set these equations equal to one another and isolate  by dividing both sides by , the mass of an object on Earth.

Using the mass of the Earth, the radius of the Earth, and the gravitational constant, , we get a value of approximately if we solve for .

The difference between the mass as measured in air and the mass as measured when it is suspended in water is the mass of the displaced water, easily reduced to the volume of the solid.

First calculate the weight of the solid in air.

In water, it weighs  The difference between these values is the buoyant force acting on the solid.

Recall that buoyant force is equal to the weight of water displaced by the object.

This is an application of Wein's Law that states the following:

, where  is the wavelength of maximum emission of the object (measured in ), and  is the temperature in . Since the wavelength and the temperature are inversely proportional, if we double the temperature, we must cut the wavelength by the same proportion. Therefore, the temperature must be halved.   

Stefan-Boltzmann's equation for a blackbody states:

, where  is the energy emitted each second,  is the Stefan-Boltzmann constant, and  is the temperature of the blackbody. Therefore, if we triple the temperature, the energy will increase by a factor of 

The kinetic theory of gas states:

. Whenever the velocity of the individual gas particles is larger than the escape speed of the planet, 

, the gas particles will leak into space and deplete the atmosphere. The physical property that determines this is the mass of the planet. 

While moving clocks do in fact record time moving at different rates, the time dilation works both ways. This means that a stationary person will view a moving clock ticking slower, but at the same time, a person moving alongside the moving clock will see the stationary clock ticking slower. However, clocks experiencing great accelerations will be permanently changed, "losing" time relative to a clock not being accelerated. Thus, the age difference occurs during the portion of the journey when the traveler accelerates at a great rate in order to return to Earth.

To derive the Schwarzschild radius of a black hole, set gravitational potential energy equal to kinetic energy at escape velocity:

Solving for mass of the black hole:

The equation for time dilation is given by:

In this problem v=0.8c T=12.  Using this equation, we get:

Adding 20 years to the age initial age of 30:

The Earth-twin is now 50.

Length contraction only occurs in the direction of motion.  This means that the x component of the length, which is cos(30), does not change; length contraction only occurs the the y component, which is sin(30).

First, we find the Lorentz factor:

Next, we apply the time dilation equation to the length in the y direction:

Finally, we find the total length by combining the length-contracted y component and the unchanged x component: