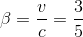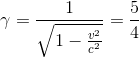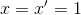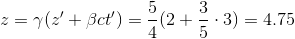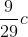GRE Subject Test: Physics : GRE Subject Test: Physics
Study concepts, example questions & explanations for GRE Subject Test: Physics
All GRE Subject Test: Physics Resources
Example Questions
Example Question #4 : Special Relativity
A rocket of length 5 meters passes an observer on earth. The observer measures the passing rocket to be 3 meters long. What is the velocity of the rocket in the reference frame of the Earth-based observer?
Length contraction is given by
Where in this case,
The Lorentz factor is given by:
Combining these two equations, we get:
Solving for v:
Example Question #1 : Special Relativity
A relativistic particle of mass m has a total energy 37 times its rest energy. What is the momentum of the particle, in units of mc?
37
21
52
98
144
37
The total energy E of a relativistic particle is related to its rest mass energy Eo by:
Where gamma is related to the momentum by:
Combining the equations and solving for p, we get:
Which, in the units specified, is 37.
Example Question #2 : Special Relativity
A particle of mass m traveling at a relativistic speed has a momentum of 50 mc. What is the total energy E of the particle, expressed in units of the rest mass energy Eo?
For a relativistic particle, momentum is given by:
from which we can solve for gamma:
Total energy of a relativistic particle is given by:
Example Question #1 : Energy And Momentum
The rest mass energy 
The question tells us:
Where the rest mass energy of a particle is:
Using the equation for the total energy of a particle, we can substitute:
Solving this for 
Which, in units of mc, gives us the correct answer.
Example Question #3 : Special Relativity
The relativistic momentum of a particle with mass 
The total energy of a relativistic particle is given by:
Substituting the momentum, we get:
Because the rest mass energy of a particle is given by:
The total energy is:
Example Question #6 : Special Relativity
A scientist measures the spectrum of relativistic jet emitted from a black hole. He finds that the a particular spectral line, which has a stationary wavelength of 212.5 nm, has a Doppler shifted wavelength of 643.7 nm. What is the radial velocity of the relativistic jet?
The relativistic Doppler shift equation is given by:
Where 
Because the stationary wavelength is shorter than the moving wavelength, the object must be receding from the Earth, eliminating two answers.
The speed of light is approximately 
Making the approximation that
Combining this with the first equation:
From beta, we can find the velocity:
Example Question #2 : Energy And Momentum
A particle in an accelerator has a total energy 
The total energy of a relativistic particle is given by:
Solving for the rest mass 
Which, in the units specified, gives the answer 3.
Example Question #1 : Four Vectors
A reference frame S' is moving at 0.6c in the z direction with respect to a stationary frame S. An event occurs in S' with the coordinates (x', y', z', ct')=(1, 0, 2, 3). What are the coordinates (x, y, z, ct) of the event with respect to the stationary frame S?
(1, 0, 2.64, 3.3)
(1, 0, 4.75, 5.25)
(1, 0, 3.3, 2.64)
(1, 0, 2, 3)
(1, 0, 5.25, 4.75)
(1, 0, 4.75, 5.25)
To apply a Lorentz transformation, we need gamma and beta:
Then, apply the Lorentz transformation:
Example Question #2 : Four Vectors
A container of water is carried on a space ship traveling at 60% the speed of light relative to the Earth. From the perspective of an observer on Earth, what is the speed of the light in the water?
The speed of light through water in a stationary frame is found from the index of refraction of water, which is approximately
To find the relative speed, use the following equation:
Example Question #1 : Fundamental Concepts
Which of the following wavelengths could be used to measure the position of an electron with the greatest accuracy?
Radio
Red light
Gamma-rays
Infared
X-ray
Gamma-rays
The Heisenberg Uncertainty principle states that
Therefore, the smallest wavelength will have the lowest uncertainty in the position. Thus, we must pick the regime of options given which has the lowest wavelength. That is gamma-ray.
Certified Tutor
Certified Tutor
All GRE Subject Test: Physics Resources
