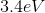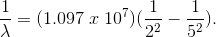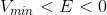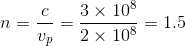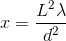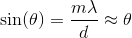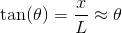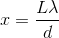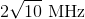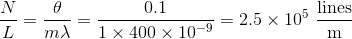The Heisenberg Uncertainty Principle states that:

 Since the uncertainty in the position is inversely proportional to the uncertainty in the momentum, we need to pick the longest wavelength. Of the options listed, radio has the longest wavelength.  

This is a fundamental concept question. For a ground state particle, the only place where the probability is equal to zero is at the boundary because the particle cannot be found there. He has to be in the box (not unlike a cat).

, where  refers to the final and initial energy levels, respectively.

However, since the question asked what is the energy of the photon, it is the absolute value of the energy calculated above because of conservation of energy. The photon carries away the energy lost by the atom. 

.

Here,  is the wavelength,  is the Rydberg constant,  for the Balmer series, and  refers to the upper atomic level (this is  in this case). Now, we just need to plug everything in, and solve for wavelength.

By inverting,  This is in the violet regime of the visible spectrum. 

For a gravitation potential, the total energy is:

, where

When the energy equals the minimum potential energy, the satellite has just enough energy to maintain a circular orbit around the planet. When the potential energy is larger than the total energy, the satellite spirals in toward the planet. When the total energy is greater than zero, the satellite is deflected out into space.

Cherenkov radiation is emitted by a particle traveling faster than the phase velocity of light in that medium. Because , the phase velocity of light in the glass is:

This is the minimum velocity of a particle to be emitting Cherenkov radiation in glass. This eliminates all answers except  and . The latter is impossible because it is greater than the speed of light in a vacuum, therefore the answer is .

The phase velocity of light through a medium with refractive index  is given by:

Solving this for  and substituting our given value of _:

The condition for constructive interference with double slit diffraction is given by:

Where  is 0, 1, 2, ...

Solving for the angle and using the small angle approximation, we get;

The distance  in the diagram can be related to the other quantities by simple geometry:

Again, with the help of the small angle approximation. Setting the two thetas equal to each other and solving for , we get:

For the central band, , so the  position is also zero. The next band, , yields a distance of:

The beat from two combined sound waves is:

The equation describing maxima of a diffraction grating is:

Where d is the separation of slits, which can also be expressed as:

Substituting d into the first equation and making the small angle approximation, one can solve for  (lines per length):

Note that the angle had to be converted from degrees to radians. Finally, the question asks for lines per centimeter, not meter, so the answer becomes .