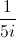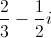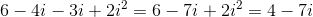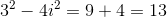To get rid of the fraction, multiply the numerator and denominator by the conjugate of the denominator.

$\displaystyle \frac{8-3i}{2-i}\left(\frac{2+i}{2+i}\right)$

Now, multiply and simplify.

$\displaystyle \frac{8-3i}{2-i}\left(\frac{2+i}{2+i}\right)=\frac{16+8i-6i-3i^2}{4-i^2}$

Remember that $\displaystyle i^2=-1$

$\displaystyle \frac{16+8i-6i-3i^2}{4-i^2}=\frac{16+2i-3(-1)}{4-(-1)}=\frac{19+2i}{5}$

Multiply both the numerator and the denominator by the conjugate of the denominator which is $\displaystyle 3-2i$ which results in

$\displaystyle \frac{\left ( 2-i \right )\left ( 3-2i \right )}{\left ( 3+2i \right )\left ( 3-2i \right )}$

The numerator after simplification give us $\displaystyle 6-4i-3i+2i^{2}=6-7i+2i^{2}=4-7i$

The denominator is equal to $\displaystyle 3^{2}-4i^{2}=9+4=13$

Hence, the final answer in standard form =

$\displaystyle \frac{4}{13}-\frac{7i}{13}$

The definition of a complex conjugate is each of two complex numbers with the same real part and complex portions of opposite sign. 

$\displaystyle In\ this\ case\ we\ have\ 3-i\sqrt{7}$

$\displaystyle to\ find\ its'\ complex\ conjugate\ we\ change\ the\ sign\ of\ the\ complex\ part$

$\displaystyle The\ complex\ conjugate\ is: 3+i\sqrt{7}$

The complex conjugate of a complex equation $\displaystyle (a+bi), \{a,b\}\in \mathbb {R}$ is $\displaystyle (a-bi)$.

The complex conjugate when multiplied by the original expression will also give me a real answer.

The complex conjugate of $\displaystyle (3+4i)$ is $\displaystyle (3-4i)$

$\displaystyle \frac{14i+4}{7i-2}$

In problems like this, you are expected to simplify by removing i from the denominator. To do this, multiply the numerator and denominator by the conjugate of the denominator (switch the sign between the two terms from either a plus to a minus or vice versa) over itself. The conjugate over itself equals 1 and does not change the value of the expression (any number multiplied by 1 is still that number). Multiplying by the conjugate is the only way to eliminate i since there will be no middle term when we foil.

$\displaystyle \frac{14i+4}{7i-2}\cdot \frac{7i+2}{7i+2}$

$\displaystyle \frac{(14i+4)(7i+2)}{(7i-2)(7i+2)}$

$\displaystyle \frac{98i^{2}+28i+28i+8}{49i^{2}-4}$

Simplify i squared to -1 and then combine like terms

$\displaystyle \frac{98(-1)+28i+28i+8}{49(-1)-4}$

$\displaystyle \frac{-98+28i+28i+8}{-49-4}$

$\displaystyle \frac{-90+56i}{-53}$

$\displaystyle \frac{2+11i}{3-4i}$

In problems like this, you are expected to simplify by removing i from the denominator. To do this, multiply the numerator and denominator by the conjugate of the denominator (switch the sign between the two terms from either a plus to a minus or vice versa) over itself. The conjugate over itself equals 1 and does not change the value of the expression (any number multiplied by 1 is still that number). Multiplying by the conjugate is the only way to eliminate i since there will be no middle term when we foil.

$\displaystyle \frac{2+11i}{3-4i}\cdot \frac{3+4i}{3+4i}$

$\displaystyle \frac{(2+11i)(3+4i)}{(3-4i)(3+4i)}$

$\displaystyle \frac{6+33i+8i+44i^{2}}{9-16i^{2}}$

Simplify i squared to be -1 and then combine like terms

$\displaystyle \frac{6+33i+8i+44(-1)}{9-16(-1)}$

$\displaystyle \frac{6+33i+8i-44}{9+16}$

$\displaystyle \frac{-38+41i}{25}$

$\displaystyle \frac{7i}{-5+4i}$

In problems like this, you are expected to simplify by removing i from the denominator. To do this, multiply the numerator and denominator by the conjugate of the denominator (switch the sign between the two terms from either a plus to a minus or vice versa) over itself. The conjugate over itself equals 1 and does not change the value of the expression (any number multiplied by 1 is still that number). Multiplying by the conjugate is the only way to eliminate i since there will be no middle term when we foil.

$\displaystyle \frac{7i}{-5+4i}\cdot \frac{-5-4i}{-5-4i}$

$\displaystyle \frac{7i(-5-4i)}{(-5+4i)(-5-4i)}$

$\displaystyle \frac{-35i-28i^{2}}{25-16i^{2}}$

Simplify i squared to be -1 and then combine like terms

$\displaystyle \frac{-35i-28(-1)}{25-16(-1)}$

$\displaystyle \frac{-35i+28}{25+16}$

$\displaystyle \frac{-35i+28}{41}$

$\displaystyle \frac{8i-2}{4i+6}$

In problems like this, you are expected to simplify by removing i from the denominator. To do this, multiply the numerator and denominator by the conjugate of the denominator (switch the sign between the two terms from either a plus to a minus or vice versa) over itself. The conjugate over itself equals 1 and does not change the value of the expression (any number multiplied by 1 is still that number). Multiplying by the conjugate is the only way to eliminate i since there will be no middle term when we foil.

$\displaystyle \frac{8i-2}{4i+6}\cdot \frac{4i-6}{4i-6}$

$\displaystyle \frac{(8i-2)(4i-6)}{(4i+6)(4i-6)}$

$\displaystyle \frac{32i^{2}-8i-48i+12}{16i^{2}-36}$

Simplify i squared to be -1 and then combine like terms

$\displaystyle \frac{32(-1)-8i-48i+12}{16(-1)-36}$

$\displaystyle \frac{-32-8i-48i+12}{-16-36}$

$\displaystyle \frac{-20-56i}{-52}$

The coefficients of all the terms can divide by 4 so reduce each of them

$\displaystyle \frac{-5-14i}{-13}$

$\displaystyle \frac{2i}{9i+3}$

In problems like this, you are expected to simplify by removing i from the denominator. To do this, multiply the numerator and denominator by the conjugate of the denominator (switch the sign between the two terms from either a plus to a minus or vice versa) over itself. The conjugate over itself equals 1 and does not change the value of the expression (any number multiplied by 1 is still that number). Multiplying by the conjugate is the only way to eliminate i since there will be no middle term when we foil.

$\displaystyle \frac{2i}{9i+3}\cdot \frac{9i-3}{9i-3}$

$\displaystyle \frac{2i(9i-3)}{(9i+3)(9i-3)}$

$\displaystyle \frac{18i^{2}-6i}{81i^{2}-9}$

Simplify i squared to be -1 and then combine like terms

$\displaystyle \frac{18(-1)-6i}{81(-1)-9}$

$\displaystyle \frac{-18-6i}{-81-9}$

$\displaystyle \frac{-18-6i}{-90}$

Since each term divides by a greatest common factor of -6 reduce all of the coefficients. It would also be equivalent to divide by 6 to reduce all of the terms.

$\displaystyle \frac{3+i}{15}$

$\displaystyle \frac{-19i-8}{-5i-2}$

In problems like this, you are expected to simplify by removing i from the denominator. To do this, multiply the numerator and denominator by the conjugate of the denominator (switch the sign between the two terms from either a plus to a minus or vice versa) over itself. The conjugate over itself equals 1 and does not change the value of the expression (any number multiplied by 1 is still that number). Multiplying by the conjugate is the only way to eliminate i since there will be no middle term when we foil.

$\displaystyle \frac{-19i-8}{-5i-2}\cdot \frac{-5i+2}{-5i+2}$

$\displaystyle \frac{(-19i-8)(-5i+2)}{(-5i-2)(-5i+2)}$

$\displaystyle \frac{95i^{2}+40i-38i-16}{25i^{2}-4}$

Simplify i squared to be -1 and then combine like terms

$\displaystyle \frac{95(-1)+40i-38i-16}{25(-1)-4}$

$\displaystyle \frac{-95+40i-38i-16}{-25-4}$

$\displaystyle \frac{-111+2i}{-29}$