Call Now to Set Up Tutoring:

(888) 888-0446

GRE Subject Test: Chemistry : General Chemistry

Study concepts, example questions & explanations for GRE Subject Test: Chemistry

Create An Account

All GRE Subject Test: Chemistry Resources

1 Diagnostic Test 152 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : Titrations

Screen shot 2015 10 25 at 8.56.18 pm

Based on the pH titration curve provided, how many acidic protons are in this acid?

Possible Answers:

Three

It cannot be determined from the graph

Four

One

Two

Correct answer:

Two

Explanation:

The equivalence point is the point in a titration at which the number of moles of titrant species equals the number of moles of analyte. For a polyprotic acid there are multiple equivalence points because there are more than one acidic proton in one molecule of the acid. A titration curve has as many equivalence points as the number of protons that may be neutralized by the interaction with a base. In this titration curve there are two equivalence points. The equivalence points occur when the graph has a very steep slope, and involve very large changes in pH with additions of small amounts of base. For this graph, the equivalence points occur at about pH 3.5 and 10.

Report an Error

Example Question #112 : General Chemistry

What volume in liters of $0.1\textup{ M}$ NaOH is needed in the titration of $50.0\textup{ mL}$ of a $0.150\textup{ M}$ $CH_{3}COOH$ (acetic acid) solution to reach the equivalence point?

Possible Answers:

$0.075\textup{ L}$

$0.025\textup{ L}$

$1.1\textup{ L}$

$0.110\textup{ L}$

$2.20\textup{ L}$

Correct answer:

$0.075\textup{ L}$

Explanation:

The equivalence point in a titration is the point in which the number of moles of titrant equals to the number of moles of analyte:

$number\ of\ moles\ of\ acetic\ acid=number\ of\ moles\ NaOH$

We need to determine the number of moles of acetic acid we are dealing with:

$50.00\ mL=0.050\ L$

$\frac{0.150\ moles}{L}\times0.050L\ acetic\ acid=0.0075\ moles\ acetic\ acid$

Therefore, at the equivalence point there are also 0.0075 moles of NaOH in the solution. In order to determine the number of moles of NaOH in solution, we must use the concentration of NaOH as a conversion factor to determine the volume added to the acetic acid solution.

$0.0075\ moles\ NaOH\times \frac{L}{0.100\ moles}=0.075\ L\ NaOH$

Report an Error

Example Question #11 : Titrations

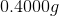
A 0.4000g sample of a monoprotic acid was titrated against a 0.05M solution of NaOH . If the end point was reached after adding $30 mL\ NaOH$ , what is the molar mass of the weak acid?

Possible Answers:

$266.67\frac{g}{mol}$

$162.11\frac{g}{mol}$

$6.0\times10^{-4}\frac{g}{mol}$

$0.0038\frac{g}{mol}$

Correct answer:

$266.67\frac{g}{mol}$

Explanation:

A pH indicator added to a solution causes a color change which is an indication that a reaction has reached the equivalence point. The equivalence point is when the number of moles of titrant equals the number of moles of analyte. The end point is an approximation of this in a titration.

At the equivalence point:

$moles\ of\ NaOH=moles\ of\ acid$

The number of moles of NaOH at equivalence point is calculated as follows:

$0.030\ L\times \frac{0.05\ moles}{L}=0.0015\ moles\ NaOH$

$moles\ of\ acid= 0.0015\ moles$

Assuming we were trying to convert the number of grams of the monoprotic acid to moles, the equation would be set up as follows:

$grams\ of\ acid\ (g) \times\ molecular\ weight\left ( \frac{moles}{g} \right )=number\ of\ moles$

Let's plug the values we have into this equation and give the molar mass a value of :

$0.4000\ g\times \frac{1\ mole}{X}=0.0015\ moles$

Rearranging this equation to solve for the molar mass gives:

$X=\frac{0.4000\ g\times\ 1\ mole}{0.0015\ moles}=266.67\ grams$

Report an Error

Example Question #21 : Acid Base Chemistry

What is the molarity of a HCl solution that has a pH of 5.0 ?

Possible Answers:

1.50 M

$5.5 * 10^{-1} M$

$1 * 10^{-5} M$

0.5M

3.50 M

Correct answer:

$1 * 10^{-5} M$

Explanation:

The pH of the solution is , therefore the concentration would be $1 * 10^{-5} M$ . This solution is based on the equation, $[H^{+}] = 10^{-pH}$ and because hydrochloric is a strong acid, it can be assumed to completely dissociate in solution.

Report an Error

Example Question #112 : Gre Subject Test: Chemistry

What is the pH of a $2.0*10^{-4} M$ solution of NaOH ?

Possible Answers:

10.3

7.8

Correct answer:

10.3

Explanation:

We need to calculate the pH of a $2*10^{-4} M$ NaOH solution. There is one mole of OH^- in every mole of NaOH , therefore:

$[OH^{-}]=2*10^{-4}\ M$

$pOH=-log(OH^{-})=-log(2*10^{-4})=3.7$

The equation with the relationship between pH and pOH is:

pH+pOH=14

We can calculate the pH by rearranging this equation:

pH= 14.00-3.7=10.3

Another way of solving this problem is shown below. The equation with the relationship between $H_{3}O^{+}$ and $OH^{-}$ concentration is:

$K_{w}=[H_{3}O^{+}][OH^{-}]=1.0*10^{-14}$

Rearrange this equation:

$[H_{3}O^{+}]=\frac{[K_{w}]}{[OH^{-}]}=\frac{1.0*10^{-14}}{2*10^{-4}}=5*10^{-11}$

We can calculate the pH of this solution using the equation below:

$pH=-log(H_{3}O^{+})=-log(5.0*10^{-11})=10.3$

Report an Error

Example Question #113 : Gre Subject Test: Chemistry

What is the pH of a $5.0*10^{-4} M$ solution of $Ca(OH)_{2}$ ?

Possible Answers:

Correct answer:

Explanation:

First we need to calculate the [OH^-] of the $5*10^{-4} M$ $Ca(OH)_{2}$ solution. For every mole of $Ca(OH)_{2}$ , there is double the number of moles of hydroxide ions:

$[OH^{-}]=2*(5 *10^{-4} M)=0.001M$

The pOH can be calculated using the below equation:

$pOH=-log(OH^{-})=-log(0.001)=3$

The equation with the relationship between pH and pOH is below:

pH+pOH=14

We can calculate the pH by rearranging this equation:

pH= 14.00-3.00=11

Another way of solving this problem is shown below. The equation with the relationship between $H_{3}O^{+}$ and $OH^{-}$ concentration is:

$K_{w}=[H_{3}O^{+}][OH^{-}]=1.0*10^{-14}$

Rearrange this equation:

$[H_{3}O^{+}]=\frac{[K_{w}]}{[OH^{-}]}=\frac{1.0*10^{-14}}{0.001}=1*10^{-11}$

We can calculate the pH of this solution using the equation below:

$pH=-log(H_{3}O^{+})=-log(1.0*10^{-11})=11$

Report an Error

Example Question #2 : P H

Considering the K_a of (hydrofluoric acid) is $6.8\times10^{-4}$ , what is the pK_b of the base F^- ?

Possible Answers:

8.4

6.4

10.8

5.5

7.5

Correct answer:

10.8

Explanation:

The relationship between K_a and K_b is:

$K_{a}*\ K_{b}=K_{w}$

$K_{w}=1.0\times10^{-14}$

Rearranging this equation gives:

$K_{b}=\frac{K_{w}}{K_{a}}=\frac{1.0\times 10^{-14}}{6.8\times 10^{-4}}=1.5\times10^{-11}$

In order to calculate the pK_b , we must use this relationship:

$pK_{b}=-log(K_{b})=-log(1.5\times 10^{-11})=10.8$

Report an Error

Example Question #31 : Acid Base Chemistry

What is the pH of a $0.05 \textup{ M}$ solution of HCl ?

Possible Answers:

11.0

0.05

5.5

4.1

1.3

Correct answer:

1.3

Explanation:

Below is the equilibria of HCl in an aqueous solution:

$HCl(l) +H_{2}O(l)\rightleftharpoons\ Cl^{-}(aq)+H_{3}O^{+}(aq)$

HCl is a strong acid so it completely ionizes in solution. It has a high $K_{eq}$ of ^.

There is 100% dissociation of HCl , therefore the resulting $H_{3}O^+$ in solution equals to the concentration of original HCl .

$[H_{3}O^{+}]=0.05M$

$pH=-log[H_{3}O^{+}]=-log[0.05]=1.3$

Report an Error

Example Question #31 : Acid Base Chemistry

What is the pH of a $0.10 \textup{ M}$ solution of NaOH ?

Possible Answers:

5.0

8.1

1.0

0.1

Correct answer:

Explanation:

Below is the equilibria of NaOH in an aqueous solution:

$NaOH(s)\rightleftharpoons\ Na^{+}(aq)+OH^{-}(aq)$

NaOH is a strong base so it completely ionizes in solution. It has a high solubility product constant.

There is 100% dissociation of NaOH , therefore the resulting $OH^{-}$ in solution equals to the concentration of original NaOH .

$[OH^{-}]=0.10M$

$pOH=-log[OH^{-}]=-log[0.10]=1$

pH+pOH=14

pH=14-pOH=14-1=13

Report an Error

Example Question #1 : P H

If $3.11\times10^{-4}\ moles$ of NaOH is reacted with $5.71\times10^{-4}\ moles$ of HCl , what is the pH if the total volume of the solution is 1 liter ?

Possible Answers:

2.1

3.6

8.4

6.6

Correct answer:

3.6

Explanation:

Based on the chemical equation, HCl and NaOH react in a 1:1 mole ratio. Therefore, in order to find the pH of this solution you must first determine the difference in moles of the two reactants and the limiting reactant. The reactant in excess will determine the pH of the solution. $5.71\times 10^{-4}\ moles\ HCl-3.11\times 10^{-4}\ moles\ NaOH=2.59\times 10^{-4}\ moles\ HCl$

There HCl is in excess and the pH of the solution will be based on the moles of the excess HCl .

$moles\ of\ H^{+}=2.59\times 10^{-4}}\ moles$

$Molarity\ [H^+]=\frac{moles\ of\ solute}{Liters\ of\ solution}=\frac{2.6\ moles}{1L}=2.6M$

$pH=-log[H^{+}]=-log[2.59\times 10^{-4}]=3.6$

Report an Error

View Tutors

Yongmao
Certified Tutor

Nankai University, Bachelor of Science, Chemistry. Washington University in St Louis, Doctor of Philosophy, Organic Chemistry.

View Tutors

Nate
Certified Tutor

University of Wisconsin-Oshkosh, non degree, Prepharmacy. University of Wisconsin-Madison, Pharmaceutical Chemist, Pharmacy.

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All GRE Subject Test: Chemistry Resources

1 Diagnostic Test 152 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Houston, English Tutors in Los Angeles, Statistics Tutors in Boston, Computer Science Tutors in Philadelphia, Math Tutors in New York City, Reading Tutors in Philadelphia, Computer Science Tutors in Miami, SAT Tutors in Seattle, GMAT Tutors in Seattle, Chemistry Tutors in Phoenix

Popular Courses & Classes

Spanish Courses & Classes in Phoenix, GMAT Courses & Classes in Philadelphia, GRE Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Los Angeles, MCAT Courses & Classes in San Diego, SAT Courses & Classes in Phoenix, LSAT Courses & Classes in Atlanta, ACT Courses & Classes in Philadelphia, ISEE Courses & Classes in Houston, SSAT Courses & Classes in Philadelphia

Popular Test Prep

SAT Test Prep in Dallas Fort Worth, GMAT Test Prep in New York City, GRE Test Prep in Denver, ACT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Chicago, ACT Test Prep in Miami, GRE Test Prep in Dallas Fort Worth, MCAT Test Prep in Seattle, ACT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

GRE Subject Test: Chemistry : General Chemistry

Study concepts, example questions & explanations for GRE Subject Test: Chemistry

All GRE Subject Test: Chemistry Resources

Example Questions

Example Question #3 : Titrations

Example Question #112 : General Chemistry

Example Question #11 : Titrations

Example Question #21 : Acid Base Chemistry

Example Question #112 : Gre Subject Test: Chemistry

Example Question #113 : Gre Subject Test: Chemistry

Example Question #2 : P H

Example Question #31 : Acid Base Chemistry

Example Question #31 : Acid Base Chemistry

Example Question #1 : P H

All GRE Subject Test: Chemistry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: