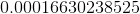GRE Math : GRE Quantitative Reasoning
Study concepts, example questions & explanations for GRE Math
All GRE Math Resources
Example Questions
Example Question #1 : How To Find Order Of Operations
Evaluate:
3 + 2(1 * 9 + 8) – 9/3
36
82
76/3
37/3
34
34
Order of operations
Do everything inside the parenthesis first:
3 + 2(17) – 9/3
next, do multiplication/division
3 + 34 – 3
= 34
Example Question #1 : How To Find Order Of Operations
3 + 4 * 5 / 10 – 2 =
5.5
3
7
5
1.5
3
Here we must use order of operations. First we multiply 4 * 5 = 20. Then 20 / 10 = 2. Now we can do the addition and substraction. 3 + 2 – 2 = 3. If you started at the beginning on the left hand side and not used order of operations, you would mistakenly choose 1.5 as the correct answer.
Example Question #1 : How To Find Order Of Operations
Order of operations can be remembered by PEMDAS (Please Excuse My Dear Aunt Sally): Parentheses Exponents Multiplication Division Addition Subtraction.
[7(5 + 2) – (5 * 8)]2 =
1: Inner parentheses = [ 7(7) – 40 ]2
2: Outer brackets = [ 49 – 40 ]2 = 92
3: Exponents = 81
Example Question #2 : How To Find Order Of Operations
This looks daunting as one long equation, but let's look at each piece and then add them all together.
2–3 = 1/23 = 1/8
250 = 1
(–218)1 = –218
6251/4 = 5
(–27)1/3 = –3
Then, 2–3 + 250 + (–218)1 + 7/8 – 6251/4 + (–27)1/3 = 1/8 + 1 – 218 + 7/8 – 5 – 3 = –224.
Example Question #1 : Percentage
What percentage of a solution is blood if it contains 
First, you must find the total amount of solution. This is 
Now, the percentage of the solution that is blood can be represented:
This is the same as 
Example Question #1 : Percentage
What is the percentage increase of an account that began with a balance of 
Recall that the formula for percentage increase is:
For our numbers, this would be:
Recall that to find a percentage from a decimal, you multiply by 
Example Question #2 : Percentage
If one of the employees across both industries were to be selected at random, what is the probability that the employee will be a construction industry worker who stayed in the same role for 5 years or more?
65%
10%
26%
17%
20%
26%
The first step is to figure out the percentage of construction employees that have stayed in the same role for 5 years or more—this would include both the "5 to 9 year" and "10+ years" ranges. This would be 0.25 + 0.4 = 65% of all construction employees. To convert to the number of employees, we take the percentage of their total, 0.65 * 8,000,000 = 5,200,000 workers. However, since the probability we are attempting to find is of workers between both industries, we must add the 8 million to the 12 million = 20 million workers total. 5,200,000/20,000,000 = 0.26, or a 26% chance.
Example Question #3 : Percentage
For every 1000 cookies baked, 34 are oatmeal raisin.
Quantity A: Percent of cookies baked that are oatmeal raisin
Quantity B: 3.4%
Quantity A is greater
The relationship cannot be determined from the information given.
The two quantities are equal.
Quantity B is greater
The two quantities are equal.
Simplify Quantity A by dividing the number of oatmeal raisin cookies by the total number of cookies to find the percentage of oatmeal raisin cookies. Since a percentage is defined as being out of 100, either multiply the resulting decimal by 100 or reduce the fraction until the denominator is 100. You will find that the two quantities are equal.
Example Question #4 : Percentage
50 students took an exam. There were 4 A's, 9 B's, 15 C's, 8 D's, and the rest of the students failed. What percent of the students failed?
which equals 28%.
Example Question #5 : Percentage
Column A: 
Column B:
Column B is greater.
Column A is greater.
The relationship cannot be determined from the given information.
The two quantities are equal.
Column B is greater.
2/5% = 0.40% = 0.004. Therefore, Column B is greater.
All GRE Math Resources
