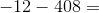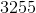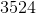Because Sam needs to make 300 pies, and each pie needs 4 apples, the number of apples he needs is

300 x 4 = 1200.

To determine how many bushels Sam needs, divide the total number of apples by the number of apples sold in a bushel.

1200 / 126 = 9.524

Because apples are sold by the whole bushel, Sam cannot order part of a bushel. In order to make sure he has sufficient apples, he will need to order 10 bushels.

In order to find a number divisible by 6, you must find a number divisible by both of its factors — 2 and 3. Only even numbers are divisible by 2, so 81 is eliminated. In order to be divisible by 3, the sum of the digits has to be divisible by 3.

The sum of the digits of 316 is  3 + 1 + 6 = 10.

For 240, the sum is 2 + 4 = 6.

For 118, the sum is 1 + 1 + 8 = 10.

Only 6 is divisible by 3.

4 is already an integer, so we need to make sure x/10 is an integer too.  

Multiples of 5 won't work. For example, 5 is a multiple of 5 but 5/10 isn't an integer. Similarly, if x/10 leaves a remainder of 5, x/10 isn't an integer. For example, 15/10 leaves a remainder of 5 and isn't an integer.  

If x/10 has no remainder, then it must be an integer. For example, 10/10 and 20/10 both leave no remainders and simplify to the integers 1 and 2, respectively. 

If the remainder of  is , we know that  could be:

Since this generates an entire list of values, we cannot know which quantity is larger.  

Do not be tricked by the question, which is trying to get you to say that they are equal!

Begin by writing out a few possible values for  and .  

Since the remainder of  is , we can list:

Since the remainder of  is , we can list:

Since  (which is ) is your smallest possible value, you know that  and  are not options.  You cannot derive either  or  from the values given.  

Therefore, the only option that is left is , which is equal to .

Calculate the difference in thousands of sales for each store individually:

Store A:  thousand

Store B:  thousand

Store C:  thousand

Stores A and B both had a 5000-book increase in sales, so A and B tie.

If it helps, for this problem, think about starting at 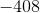 and moving twelve places in a negative direction away from zero.  

Also you can think to add 408 with 12 and then multiply that number by a negative one. Starting with the ones place eight plus two gives ten so we keep the zero in the ones place and carry the one to the tens place. Then we add one plus one to give us a two in the tens column. Next we have a four in the hundreds place. This gives us 420. Now we multiply this by negtive one to get our final answer of -420.

Whenever you subtract a negative number, you flip the sign and add:

There are 50 positive, odd numbers less than 100, and 45 of them are 2 digit numbers.

Since:

1. There are only 9 integers between 0 and 10
2. x, y, and z must all be unique
3. They must be specifically ordered such that x < y < z

There are actually not too many ways in which these numbers can be chosen. So what we can do is find a range of answers for Quantity B, and see if 6 falls a) below b) above or c) in between the range.

For the maximum:

Note that the term (x + y) is maximized when x and y are maximum. The (–z) term is maximized when z is minimized. However, there are 2 terms in (x + y) and one term in (–z); thus intuitively it seems we should prioritize (x+y). To make x and y maximum:

0 < 7 < 8 < 9 < 10 since x, y, and z must be unique.

Thus maximum: (x + y – z) = 7 + 8 – 9 = 6

For the minimum:

Note that (x + y) is minimum when (x) and (y) are minimum, and (–z) is minimum when (z) itself is maximimized. However since there are 2 terms in (x+y) and1 of (–z) , again intuititively you should prioritize  (x+y) over (-z). Then in order to make this the least number possible, x and y would be:

min(x + y – z) = 1 + 2 – 9 = –6  

Thus, the range of possible answers is:

(x + y – z): [–6, 6] 

and –7 is always less than this amount.