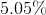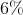All GRE Math Resources
Example Questions
Example Question #1 : Sales Tax
If a sweater has a total cost of after tax, what is the cost of the sweater before tax, if the sales tax is ?
The total cost of the sweater is the original cost plus a 4.5% tax, which can be expressed in the equation:
Where TC is the total cost, C is the original cost, and T is the tax. Now, we will plug in the information we know. Since the original cost of the sweater is unknown, we will use the variable x.
.045 is the decimal expression of 4.5%.
Now, solve for x. Consolidate the x variable.
Divide both sides by 1.045.
is the cost of the sweater before tax.
Example Question #1 : Sales Tax
A cake order cost before tax. If the tax rate is , what is the price of the cake after tax is applied?
Remember: For all percentage problems, you need to convert your percentage to a decimal before working on your equation.
You can solve this problem one of two ways. The first way, which is less efficient, is to multiply the original amount by the tax rate and then add that to the original:
or:
The easier way to do this is to multiply your original amount by plus the tax rate. (This does the addition for you in one step.)
or:
Notice that your problem is asking for the total new cost, not the amount of tax to be added!
Example Question #1 : Sales Tax
A can of rare beans costs after tax and before. What is the tax rate on this item?
Remember: For all percentage problems, you need to convert your percentage to a decimal before working on your equation.
The easiest way to solve this problem is to convert it into a clear sentence. The question is asking, "What percentage of is ?" This is the same thing as writing:
(Recall, "of" becomes multiplication and "is" becomes equals.)
Solve this by dividing both sides by :
This means that is of . In other words, it is a increase to . This is the tax rate.
Example Question #4 : How To Find The Amount Of Sales Tax
How much tax is charged on a umbrella if its tax rate is ?
Remember: For all percentage problems, you need to convert your percentage to a decimal before working on your equation.
This problem is very simple, for you only have to compute the tax amount in dollars—not the complete price.
Therefore, you merely need to multiply the original price by the tax rate.
This gives you:
Example Question #2 : Sales Tax
In the past year, the price for a bottle of water decreased by while the sales tax on the bottle of water is of the original rate. What percentage does the tax increase/decrease by compared to last year?
For this problem, we are given no numbers to work with. Therefore, we can substitute a number of our choosing into the problem. For simplicities sake, the number chosen will be $100. If the price of water decreased by 10%, that would mean that the new price for water if the old price was $100 is $90. Because tax increased by 5%, that would mean that for a bottle of water, if we assume the old tax rate was 10%, the new tax rate is 10.5%. This would mean that if previously, if you paid 10% tax for a $100 bottle of water, you would pay $10 in taxes.
Now, you would pay 10.5% tax for a $90 bottle of water meaning you would pay $9.45 in tax.
This problem asks you for the percentage the tax changes by, therefore in order to find the percent change, we divide the new tax by the old tax, or 94.5%. This means that the amount of tax paid has decreased by 5.5% compared to the following year.
Example Question #3 : Sales Tax
A supermarket sells apples for . If you buy more than of apples at once, the supermarket will discount the price by . How much will of apples cost? Round to the nearest cent.
In this problem, we are asked to find the price of of apples. The original price of apples is stated to be . That would mean that of apples would cost . Because the supermarket gives a discount if you buy of apples at once, . Rounded to the nearest cent, 13 pounds of apples would cost .
Example Question #1 : How To Find Simple Interest
Harry borrowed $5000 from his parents at a rate of simple interest of 2% annually and paid it back in full in 30 months. What is the total amount of interest and principal his parents charged him?
none of these
Principal = $5000 (original amount)
Interest = 30 months = 2 years and a half
half a year's interest is
Total interest =
Example Question #2 : How To Find Simple Interest
What is the simple interest rate on an account that accrued after a year if the original deposit was ? Round your answer to the nearest hundredth.
The easiest way to do this is to translate the question into "is / of language." The question is asking, "What percentage of is ?" Remember, is means equals and of indicates multiplication. "What" means a variable like . Therefore, we can rewrite our sentence as:
Solving for , we get:
This is %. Rounding to the nearest hudredth, you get or .
Example Question #3 : How To Find Simple Interest
What is the interest rate on an account if an original balance of rises to after one year if it is only compounded yearly?
You can solve this by using the standard formula for simple interest (which is merely a derivative of standard applications of the formulas used for percentages in general). For our problem this is:
Divide both sides by , but leave the fractions for the time being:
Solve for :
This is:
Which is the same as:
%, or % when rounded.
Example Question #4 : Interest
If a student borrows $200,000 at an interest rate of 6% compounded annually, when she graduates in 4 years how much money will she owe? Round to the nearest dollar.
$257,543
$243,432
$252,495
$265,432
$264,432
$252,495
This problem requires knowledge of the compound interest formula, .
Where is the amount of money owed, is the sum borrowed, is the yearly interest rate, is the amount of times the interest is compounded per year, and is the number of years. We know that the student borrowed $200,000 compounded annually at a %6 interest rate, therefore by plugging in those numbers we find that after she graduates in 4 years she will owe $252,495.
All GRE Math Resources