GRE Math : GRE Quantitative Reasoning

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #53 : Geometry

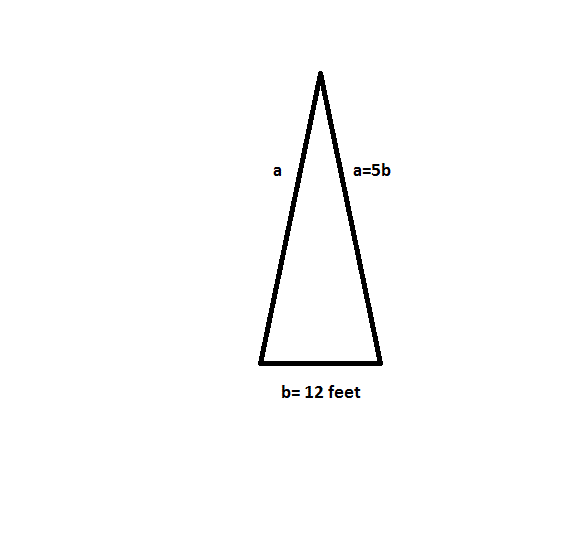
Isos._cont._gre

Find the perimeter of the acute Isosceles triangle shown above.

Possible Answers:

$\small \small 60$

$\small 133$

$\small 132$

$\small 120$

$\small 130$

Correct answer:

$\small 132$

Explanation:

To solve this problem apply the formula: $\small p=2a+b$ .

However, first calculate the length of the missing side by:

$\small p=2(a)+12$

$\small a=12\times5=60$

$\small p=2(60)+12$

$\small p=120+12=132$

Report an Error

Example Question #1 : Triangles

An obtuse Isosceles triangle has two sides with length and one side length . The length of side $\frac{3}{4}$ ft. If the length of half the length of side , what is the perimeter of the triangle?

Possible Answers:

$1\frac{1}{3}$ ft

$1\frac{1}{2}$ ft

$1\frac{2}{3}$ ft

$\frac{12}{4}$ ft

Correct answer:

$1\frac{1}{2}$ ft

Explanation:

By definition, an Isosceles triangle must have two equivalent side lengths. Since we are told that $b=\frac{3}{4}$ ft and that the sides with length are half the length of side , find the length of by: $\frac{3}{4}=\frac{6}{8}$ and half of $\frac{6}{8}=\frac{3}{8}$ . Thus, both of sides with length must equal $\frac{3}{8}$ ft.

Now, apply the formula: p=2a+b .

$p=\frac{3}{8}+\frac{3}{8}+\frac{6}{8}=\frac{12}{8}$

Then, simplify the fraction/convert to mixed number fraction:

$\frac{12}{8}=\frac{3}{2}=1\frac{1}{2}$

Report an Error

Example Question #1 : Triangles

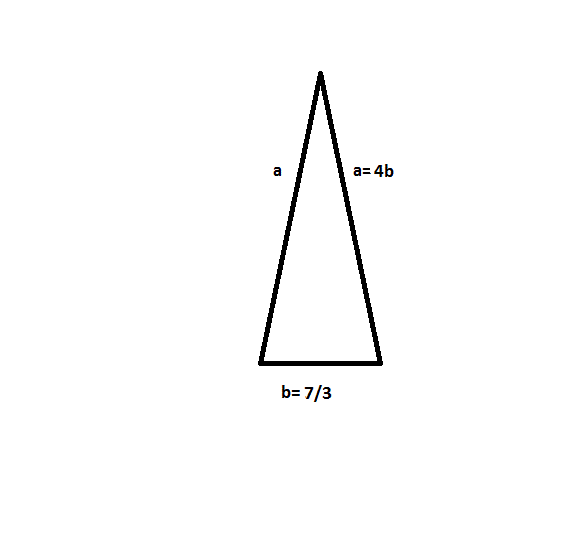
Isos._cont._gre

Find the perimeter of the acute Isosceles triangle shown above.

Possible Answers:

$\small \frac{35}{3}$

$\small 27$

$\small 18$

$\small 21$

$\small \frac{56}{3}$

Correct answer:

$\small 21$

Explanation:

In order to solve this problem, first find the length of the missing sides. Then apply the formula: $\small p=2a+b$

Each of the missing sides equal:

$\small a=\frac{7}{3}\times4=\frac{28}{3}$

Then apply the perimeter formula:
$\small p=\frac{28}{3}+\frac{28}{3}+\frac{7}{3}=\frac{63}{3}=21$

Report an Error

Example Question #1 : How To Find The Perimeter Of An Acute / Obtuse Isosceles Triangle

Isos._gre_series_

An acute Isosceles triangle has two sides with length and one side length . The length of side $\small a=$ inches. If the length of $\small b=$ $\sqrt[3]{a}$ , what is the perimeter of the triangle?

Possible Answers:

inches

Correct answer:

inches

Explanation:

In order to solve this problem, first find the length of the missing sides. Then apply the formula: $\small p=2a+b$

The missing side equals:

$b=\sqrt[3]{a}=\sqrt[3]{8}=2$

Then plug each side length into the perimeter formula:

p=2(8)+2=16+2=18

Report an Error

Example Question #62 : Geometry

Isos._gre_series_

An acute Isosceles triangle has two sides with length and one side length . The length of side $\small a=$ $\sqrt{144}$ inches. If the length of $\small b=a\times \frac{1}{2}$ , what is the perimeter of the triangle?

Possible Answers:

$\small 32$ inches

$\small 18$ inches

$\small 2$ feet

$\small 2.7$ feet

$\small 30$ inches

Correct answer:

$\small 30$ inches

Explanation:

In order to solve this problem, first find the length of the missing sides. Then apply the formula: $\small p=2a+b$

The missing side equals:

$\small a=\sqrt{144}=12$

$\small b=12\times \frac{1}{2}=\frac{12}{2}=6$

Then, apply the perimeter formula by plugging in the side values:

$\small p=2(12)+6=24+6=30$

Report an Error

Example Question #63 : Geometry

An acute Isosceles triangle has two sides with length and one side length . The length of side $\small a=$ $\small \small \frac{3}{12}$ ft. If the length of $\small b=\small a\times \frac{1}{3}$ , what is the perimeter of the triangle?

Possible Answers:

$\small \frac{9}{12}$ foot

$\small \frac{3}{4}$ foot

$\small \frac{1}{4}$ foot

$\small 6$ inches

$\small 7$ inches

Correct answer:

$\small 7$ inches

Explanation:

To solve this problem apply the formula: $\small p=2a+b$ .

However, first calculate the length of the missing side by:

$\small \frac{3}{12}+\frac{3}{12}+(\frac{3}{12}\times\frac{1}{3})$ , Note that $\small \frac{3}{36}=\frac{1}{12}$

$\small \small \frac{6}{12}+\frac{3}{36}=\frac{6}{12}+\frac{1}{12}=\frac{7}{12}$ .

Since, it takes $\small 12$ inches to make one foot, the perimeter is equal to $\small 7$ inches.

Report an Error

Example Question #64 : Geometry

An acute Isosceles triangle has two sides with length and one side length . The length of side $\small a=$ $\small 8$ inches. The length of side $\small b=$ $\small a\times \frac{1}{4}$ . Find the perimeter of the triangle.

Possible Answers:

$\small 18$ inches

$\small 19$ inches

$\small 14$ inches

$\small 13$ inches

$\small 12$ inches

Correct answer:

$\small 18$ inches

Explanation:

To find the perimeter of this triangle, apply the formula:

$\small p=2a+b$

$\small p=2(8)+(8\times \frac{1}{4})$

$\small p=16+\frac{8}{4}$

$\small p=16+2=18$

Note: Since this is an acute Isosceles triangle, the length of the base must be smaller than the length of both of the equivalent sides.

Report an Error

Example Question #11 : Isosceles Triangles

Isos._cont._gre

The obtuse Isosceles triangle shown above has two sides with length and one side length . The length of side $\small a=$ $\small 43$ inches. Side length $\small b=2a$ . Find the perimeter of the triangle.

Possible Answers:

$\small 172$ inches

$\small 86$ inches

$\small 84$ inches

$\small 15\sqrt{2}$ inches

$\small 129$ inches

Correct answer:

$\small 172$ inches

Explanation:

To find the perimeter of this triangle, apply the perimeter formula:

$\small p=2a+b$

Since, $\small a=43$ , and $\small b=2a$ then $\small b$ must have a value of: $\small 2\times43=86$

This triangle has two side lengths of $\small 43$ inches, and one side length of $\small 86$ inches.

Thus, the solution is:

$\small p=2(43)+86=172$

Report an Error

Example Question #1251 : Gre Quantitative Reasoning

A triangle has two sides with length and one side length . The length of side $\frac{1}{4}$ yard. If the length of the length of side , what is the perimeter of the triangle?

Possible Answers:

$\small \frac{6}{12}$ yard

$\frac{5}{4}$ yard

$\small \frac{1}{4}$ yard

$\small \frac{7}{12}$ yard

$\small \frac{1}{3}$ yard

Correct answer:

$\frac{5}{4}$ yard

Explanation:

The first step to solving this problem is that we must find the length of length $\small a.$ Since, $\small a$ is $\small 2$ 4 the length of side $\small b$ , use the following steps:

$\small \small b=\frac{1}{4}$
$\small a=\frac{1}{4}\times2=\frac{1}{2}$

Now, apply the formula: $\small p=2a+b$

$\small p=\frac{2}{4}+\frac{2}{4}+\frac{1}{4}=\frac{5}{4}$

Report an Error

Example Question #11 : Triangles

An isosceles triangle has an angle of 110°. Which of the following angles could also be in the triangle?

Possible Answers:

110

Correct answer:

Explanation:

An isosceles triangle always has two equal angles. As there cannot be another 110° (the triangle cannot have over 180° total), the other two angles must equal eachother. 180° - 110° = 70°. 70° represents the other two angles, so it needs to be divided in 2 to get the answer of 35°.

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Los Angeles, LSAT Tutors in San Diego, Computer Science Tutors in Boston, ACT Tutors in Dallas Fort Worth, French Tutors in Los Angeles, GMAT Tutors in New York City, ACT Tutors in San Diego, ISEE Tutors in Seattle, Algebra Tutors in Seattle, Math Tutors in San Francisco-Bay Area

Popular Courses & Classes

ISEE Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Los Angeles, SSAT Courses & Classes in Denver, GMAT Courses & Classes in Miami, MCAT Courses & Classes in Philadelphia, SAT Courses & Classes in Chicago, MCAT Courses & Classes in Washington DC, ACT Courses & Classes in Miami, SAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Seattle

Popular Test Prep

ACT Test Prep in Boston, GMAT Test Prep in Seattle, GRE Test Prep in Phoenix, MCAT Test Prep in New York City, MCAT Test Prep in Boston, ISEE Test Prep in Phoenix, SAT Test Prep in Denver, ACT Test Prep in Philadelphia, LSAT Test Prep in Houston, ISEE Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : GRE Quantitative Reasoning

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #53 : Geometry

Example Question #1 : Triangles

Example Question #1 : Triangles

Example Question #1 : How To Find The Perimeter Of An Acute / Obtuse Isosceles Triangle

Example Question #62 : Geometry

Example Question #63 : Geometry

Example Question #64 : Geometry

Example Question #11 : Isosceles Triangles

Example Question #1251 : Gre Quantitative Reasoning

Example Question #11 : Triangles

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details