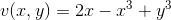Call Now to Set Up Tutoring:

(888) 888-0446

Complex Analysis : Complex Analysis

Study concepts, example questions & explanations for Complex Analysis

Create An Account

All Complex Analysis Resources

1 Diagnostic Test 13 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #21 : Complex Analysis

Given a complex number z=a+bi , under what conditions is the following equation true?

$\overline{z}=z$

Possible Answers:

The equation is only true if $\vert z\vert>1$ .

The equation is only true if a=0 .

The equation is only true if b=0 .

The equation is never true.

The equation is always true.

Correct answer:

The equation is only true if b=0 .

Explanation:

$\overline{z}$ denotes the conjugate of and is defined as
$\ovelrine{z}=a-bi$ .

Substituting this into the equation and simplifying yields:
$\begin{align*} a-bi&=a+bi\\ a-bi-a-bi&=0\\ -2bi&=0\\ b&=0. \end{align*}$

So the equation is only true if b=0 .

Report an Error

Example Question #22 : Complex Analysis

What is the value of $\vert e^{i\theta}\vert$ , where $-\pi<\theta\leq\pi$ is in radians?

Possible Answers:

Not enough information is given.

Correct answer:

Explanation:

The magnitude of a complex number $z=re^{i\theta}$ is defined as
$\vert z\vert=r$ .

If $z=e^{i\theta}$ , then r=1 , so $\vert e^{i\theta}\vert$ =1.

Report an Error

Example Question #23 : Complex Analysis

Which of the following is equivalent to this expression?

$(\sqrt3+i)^5$

Possible Answers:

$16+\sqrt3i$

$5\sqrt3+5i$

$9\sqrt3+i$

32-i

None of these

Correct answer:

None of these

Explanation:

Note that $\sqrt3+i$ lies in the first quadrant of the complex plane.

Any nonzero complex number a+bi can be written in the form $re^{\theta i}$ , where
r^2=a^2+b^2 and
$\tan(\theta)=\frac{b}{a}$ .
(We stipulate that $-\pi<\theta\leq\pi$ is in radians.)

Conversely, a nonzero complex number $re^{\theta i}$ can be written in the form a+bi , where
$a=r\cos(\theta)$ and
$b=r\sin(\theta)$ .

We can convert $\sqrt3+i$ by using the formulas above:
$r^2=a^2+b^2=(\sqrt3)^2+1^2=3+1=4$
$r=\sqrt4=2$ ,
and
$\tan(\theta)=\frac{b}{a}=\frac{1}{\sqrt3}$
$\theta=\frac{-7\pi}{6},\frac{\pi}{6}$

Since $\frac{\pi}{6}$ lies in the first quadrant of the complex plane, as does $\sqrt3+i$ , $\theta = \frac{\pi}{6}$ .

So $\sqrt3+i=2e^{\frac{\pi}{6}i}$ .

We now substitute this into our original expression and expand.
$\begin{align*} (3+i)^5&=(2e^{\frac{\pi}{6}i})^5\\ &=2^5e^{5\frac{\pi}{6}i}\\ &=32e^{\frac{5\pi}{6}i} \end{align*}$ .

Finally, we convert this number back to the form a+bi .
$a=r\cos(\theta)=32\cos(\frac{5\pi}{6})=32(\frac{-\sqrt3}{2})=-16\sqrt3$
$b=r\sin(\theta)=32\sin(\frac{5\pi}{6})=32(\frac{1}{2})=16$

So our final answer is $-16\sqrt3+16i$ .

Report an Error

Example Question #24 : Complex Analysis

Which of the following is equivalent to this expression?

$\left(\frac{\sqrt2}{2}+\frac{\sqrt2}{2}i\right)^{10}$

Possible Answers:

$\frac{\sqrt2}{8}+\frac{\sqrt2}{8}i$

$4\sqrt2i$

$-\frac{1}{32}$

None of these

Correct answer:

Explanation:

Note that $\frac{\sqrt2}{2}+\frac{\sqrt2}{2}i$ lies in the first quadrant of the complex plane.

Any nonzero complex number a+bi can be written in the form $re^{\theta i}$ , where
r^2=a^2+b^2 and
$\tan(\theta)=\frac{b}{a}$ .
(We stipulate that $-\pi<\theta\leq\pi$ is in radians.)

Conversely, a nonzero complex number $re^{\theta i}$ can be written in the form a+bi , where
$a=r\cos(\theta)$ and
$b=r\sin(\theta)$ .

We can convert $\frac{\sqrt2}{2}+\frac{\sqrt2}{2}i$ by using the formulas above:
$r^2=a^2+b^2=\left(\frac{\sqrt2}{2}\right)^2+\left(\frac{\sqrt2}{2}\right)^2=\frac{1}{2}+\frac{1}{2}=1$
$r=\sqrt1=1$ ,
and
$\tan(\theta)=\frac{b}{a}=\frac{\frac{\sqrt2}{2}}{\frac{\sqrt2}{2}}=1$
$\theta=\frac{-3\pi}{4},\frac{\pi}{4}$

Since $\frac{\pi}{4}$ lies in the first quadrant of the complex plane, as does $\frac{\sqrt2}{2}+\frac{\sqrt2}{2}i$ , $\theta=\frac{\pi}{4}$ .

So $\frac{\sqrt2}{2}+\frac{\sqrt2}{2}i=e^{\frac{\pi}{4}i}$ .

We now substitute this into our original expression and expand.
$\begin{align*} \left(\frac{\sqrt2}{2}+\frac{\sqrt2}{2}\right)^{10}&=(e^{\frac{\pi}{4}i})^{10}\\ &=e^{\frac{10\pi}{4}i} \end{align*}$ .
Because $-\pi<\theta\leq\pi$ , we substitute $\frac{10\pi}{4}$ with the coterminal angle $\frac{2\pi}{4}=\frac{\pi}{2}$ .
$\left(\frac{\sqrt2}{2}+\frac{\sqrt2}{2}i\right)^{10}=e^{\frac{\pi}{2}i}$ .

Finally, we convert this number back to the form a+bi .
$a=r\cos(\theta)=\cos(\frac{\pi}{2})=0$
$b=r\sin(\theta)=\sin(\frac{\pi}{2})=1$

So our final answer is 0+1i=i .

Report an Error

Example Question #25 : Complex Analysis

$(-\sqrt2+\sqrt2i)(\frac{i}{4})(z)=1,$

then what is the value of ?

Possible Answers:

$-\sqrt2+\sqrt2i$

-2-2i

None of these

$2\sqrt2i$

$\frac{\sqrt2}{2}-\frac{\sqrt2}{2}i$

Correct answer:

$-\sqrt2+\sqrt2i$

Explanation:

Note that the on the right side of the equation can be written as $e^{0i}$ .

Multiplying the first two terms on the left side yields
$(-\sqrt2+\sqrt2i)(\frac{i}{4})=\frac{-\sqrt2}{4}-\frac{\sqrt2}{4}i$ .
Note that this number lies in the third quadrant of the complex plane.

We now convert $-\frac{\sqrt2}{4}-\frac{\sqrt2}{4}i$ from the form a+bi to the form $re^{i\theta}$ using the identities
r^2=a^2+b^2 and
$\tan(\theta)=\frac{b}{a}$ .
$r^2=a^2+b^2=\left(-\frac{\sqrt2}{4}\right)^2+\left(-\frac{\sqrt2}{4}\right)^2=\frac{2}{16}+\frac{2}{16}=\frac{4}{16}=\frac{1}{4}$
$r=\sqrt{\frac{1}{4}}=\frac{1}{2}$
$\tan(\theta)=\frac{b}{a}=\frac{-\frac{\sqrt2}{4}}{-\frac{\sqrt2}{4}}=1$
$\theta=-\frac{3\pi}{4},\frac{\pi}{4}$ .
Since $-\frac{3\pi}{4}$ lies in the third quadrant of the complex plane, as does $-\frac{\sqrt2}{4}-\frac{\sqrt2}{4}i$ , $\theta=-\frac{3\pi}{4}$ .
So our new form is $\frac{1}{2}e^{-\frac{3\pi}{4}i}$ .

Our equation now reduces to
$(\frac{1}{2}e^{-\frac{3\pi}{4}i})(z)=e^{0i}$ .
We solve for z by dividing.
$\begin{align*} z&=\frac{e^{0i}}{\frac{1}{2}e^{-\frac{3\pi}{4}i}}\\ &=\frac{1}{\frac{1}{2}}e^{0i-\frac{-3\pi}{4}i}\\ &=2e^{\frac{3\pi}{4}i}. \end{align*}$

Finally, we convert this to the form a+bi by using the identities
$a=r\cos(\theta)$ and
$b=r\sin(\theta)$ .
$a=r\cos(\theta)=2\cos(\frac{3\pi}{4})=2(-\frac{\sqrt2}{2})=-\sqrt2$
$b=r\sin(\theta)=2\sin(\frac{3\pi}{4})=2(\frac{\sqrt2}{2})=\sqrt2$ .

So our final answer is $z=-\sqrt2+\sqrt2i$ .

Report an Error

Example Question #26 : Complex Analysis

Given a complex number z=a+bi , under what conditions is the following equation true?

$\overline{z}=-z$

Possible Answers:

The equation is only true if b=0 .

The equation is only true if $\vert z\vert = \vert\overline{z}\vert$ .

The equation is only true if a=b .

The equation is never true.

The equation is only true if a=0 .

Correct answer:

The equation is only true if a=0 .

Explanation:

$\overline{z}$ denotes the conjugate of and is defined as
$\ovelrine{z}=a-bi$ .

Substituting this into the equation and simplifying yields:
$\begin{align*} a-bi&=-(a+bi)\\ a-bi&=-a-bi\\ a-bi+a+bi&=0\\ 2a&=0\\ a&=0 \end{align*}$

So the equation is only true if a=0 .

Report an Error

Example Question #1 : Complex Functions

What does the sum below equal?

$\sum_{n=1}^{m}(e^{2\pi i/m})^{n}$

Another way of asking this question is what is the sum of the roots of unity.

$m\in \mathbb{N}$

Possible Answers:

$\pi$

$e^\pi$

Correct answer:

Explanation:

As messy as it looks, this is just a geometric series.

we will use the partial sum formula for the geometric series.

$S_{n}=\frac{a_{1}(1-r^n)}{1-r}$

$a_{1}=e^{2\pi i/m}$

$r=e^{2\pi i/m}$

$S_{m}=\frac{a_{1}(1-r^m)}{1-r}=\frac{e^{2\pi i/m}(1-{\color{Red} (e^{2\pi i/m})^m})}{1-e^{2\pi i/m}}$

the red part is the only part that matters....the m's cancel out leaving....

$S_{m}=\frac{a_{1}(1-r^m)}{1-r}=\frac{e^{2\pi i/m}(1-{\color{Red} (e^{2\pi i})})}{1-e^{2\pi i/m}}$

and...

$e^{2\pi i}=1$

thus we have...

$S_{m}=\frac{a_{1}(1-r^m)}{1-r}=\frac{e^{2\pi i/m}(1-{\color{Red} (1)})}{1-e^{2\pi i/m}}$

which gives the answer of zero.

$S_{m}=0$

Report an Error

Example Question #1 : Complex Functions

Consider the function f(z) = |z|^2

Find an expression for f'(z) (hint: use the definition of derivatve) and where it exists in the complex plane.

Possible Answers:

$f'(z) = 2|z| \text{ } \forall z$

$f'(z) = 2z \text{ } \forall z$

$f'(z) = 2z \text{ where } z=0$

$f'(z) = 0 \text{ where } z=0$

$f'(z) = 2|z| \text{ where } z=0$

Correct answer:

$f'(z) = 0 \text{ where } z=0$

Explanation:

Applying the definition of derivative, we have that

$f'(z) = \lim_{\Delta z \to 0} \frac{f(z+\Delta z) - f(z)}{\Delta z} \\$

$f'(z) = \lim_{\Delta z \to 0}\frac{|z+\Delta z|^2 - |z|^2}{\Delta z} = \lim_{\Delta z \to 0} \frac{(z+\Delta z)(\bar{z}+\overline{\Delta z}) - z\overline{z}}{\Delta z} = \lim_{\Delta z \to 0} \overline{z} + \overline{\Delta z} + z \frac{\overline{\Delta z}}{\Delta z}$

If the limits exists, it can be found by letting $\Delta z$ approach in any manner.

In particular, if we it approach through the points $(\Delta x , 0 )$ , we have that

$\overline{\Delta z} = \overline{\Delta x + i0} = \Delta x - i0 = \Delta x + i0 = \Delta z$

A similar approach with $(0, \Delta y)$ implies that $\overline{\Delta z } = -\Delta z$

Since limits are unique, these two approaches imply that

$\overline{z} + z = \overline{z} - z$ , which implies z=0 and f'(z) cannot exist when $z \neq 0$

Report an Error

Example Question #1 : Analytic And Harmonic Functions

Find a Harmonic Conjugate v(x,y) of u(x,y) = 2x-x^3+3xy^2

Possible Answers:

v(x,y) = 2-3x^2+y^3

v(x,y) = 2x-x^3+y^3

v(x,y) = 2y-x^3y+3xy^2

v(x,y) = 2y-x^2y + y^3

v(x,y) = 2y-3x^2y+y^3

Correct answer:

v(x,y) = 2y-3x^2y+y^3

Explanation:

v(x,y) is said to be a harmonic conjugate of u(x,y) if their are both harmonic in their domain and their first order partial derivatives satisfy the Cauchy-Riemann Equations. Computing the partial derivatives

u_x(x,y) = 2-3x^2+3y^2 = v_y(x,y)

v(x,y) = 2y-3x^2y+y^3 + C

where is any arbitrary constant.

Report an Error

Example Question #2 : Analytic And Harmonic Functions

Given $f(z) = z - \bar{z}$ , where does f'(z) exist?

Possible Answers:

y = 0

x = 0

Nowhere

The Entire Complex Plane

z=0

Correct answer:

Nowhere

Explanation:

Rewriting f(z) in real and complex components, we have that

$f(z) = z- \bar{z} = (x+yi) - (x-yi) = 2yi$

So this implies that f(z) = f(x + yi) = u(x,y) + v(x,y)i

where $u(x,y) = 0 \text{ and } v(x,y) = 2y$

Therefore, checking the Cauchy-Riemann Equations, we have that

$u_x(x,y) = 0 \neq v_y(x,y) = 2$

So the Cauchy-Riemann equations are never satisfied on the entire complex plane, so f(z) is differentiable nowhere.

Report an Error

View Tutors

Emmanuel
Certified Tutor

Baylor University, Bachelor of Science, Biology, General.

View Tutors

Victor
Certified Tutor

University of Baltimore, Bachelor, Law. University of Maryland-University College, Master of Arts, Management Science.

View Tutors

Joseph
Certified Tutor

Bank Street College of Education , Master's/Graduate, Early Childhood and Childhood General Education.

All Complex Analysis Resources

1 Diagnostic Test 13 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Los Angeles, SSAT Tutors in Miami, Biology Tutors in Dallas Fort Worth, Algebra Tutors in Houston, GRE Tutors in Dallas Fort Worth, Statistics Tutors in San Francisco-Bay Area, SSAT Tutors in Boston, Computer Science Tutors in Denver, Biology Tutors in Philadelphia, MCAT Tutors in Chicago

Popular Courses & Classes

MCAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Boston, ACT Courses & Classes in San Diego, Spanish Courses & Classes in Houston, SAT Courses & Classes in Seattle, GMAT Courses & Classes in Washington DC, SSAT Courses & Classes in Washington DC, SSAT Courses & Classes in San Diego

Popular Test Prep

GMAT Test Prep in Boston, GRE Test Prep in San Diego, MCAT Test Prep in Miami, ACT Test Prep in San Diego, MCAT Test Prep in Chicago, SSAT Test Prep in Atlanta, SAT Test Prep in Philadelphia, SSAT Test Prep in Dallas Fort Worth, LSAT Test Prep in New York City, LSAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Complex Analysis : Complex Analysis

Study concepts, example questions & explanations for Complex Analysis

All Complex Analysis Resources

Example Questions

Example Question #21 : Complex Analysis

Example Question #22 : Complex Analysis

Example Question #23 : Complex Analysis

Example Question #24 : Complex Analysis

Example Question #25 : Complex Analysis

Example Question #26 : Complex Analysis

Example Question #1 : Complex Functions

Example Question #1 : Complex Functions

Example Question #1 : Analytic And Harmonic Functions

Example Question #2 : Analytic And Harmonic Functions

All Complex Analysis Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: