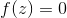All Complex Analysis Resources
Example Questions
Example Question #1 : Residue Theory
Cauchy's Residue Theorem is as follows:
Let 




For the following problem, use a modified version of the theorem which goes as follows:
Residue Theorem
If a function 

Brown, J. W., & Churchill, R. V. (2009). Complex variables and applications. Boston, MA: McGraw-Hill Higher Education.
Use the Residue Theorem to evaluate the integral of

in the region 
0
0
Note,
Thus, seeking to apply the Residue Theorem above for 


Observe,
The coefficient of 

Thus,
![\text{Res}_{z=0} [\frac{1}{z^2}f(\frac{1}{z})] = 0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067288/gif.latex)
Therefore, by the Residue Theorem above,
Hence,
Example Question #1 : Residue Theory
Cauchy's Residue Theorem is as follows:
Let 




For the following problem, use a modified version of the theorem which goes as follows:
Residue Theorem
If a function 

Brown, J. W., & Churchill, R. V. (2009). Complex variables and applications. Boston, MA: McGraw-Hill Higher Education.
Use the Residue Theorem to evaluate the integral of

in the region 
Note,
Thus, seeking to apply the Residue Theorem above for 


Observe,
The coefficient of 

Thus,
![\text{Res}_{z=0} [\frac{1}{z^2}f(\frac{1}{z})] = 5](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067280/gif.latex)
Therefore, by the Residue Theorem above,
Hence,
Example Question #5 : Residue Theory
Cauchy's Residue Theorem is as follows:
Let 




For the following problem, use a modified version of the theorem which goes as follows:
Residue Theorem
If a function 

Brown, J. W., & Churchill, R. V. (2009). Complex variables and applications. Boston, MA: McGraw-Hill Higher Education.
Use the Residue Theorem to evaluate the integral of

in the region 
Note,
Thus, seeking to apply the Residue Theorem above for 


Observe,
The coefficient of 

Thus,
![\text{Res}_{z=0} [\frac{1}{z^2}f(\frac{1}{z})] = 0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067182/gif.latex)
Therefore, by the Residue Theorem above,
Hence,
Example Question #2 : Residue Theory
Cauchy's Residue Theorem is as follows:
Let 




For the following problem, use a modified version of the theorem which goes as follows:
Residue Theorem
If a function 

Brown, J. W., & Churchill, R. V. (2009). Complex variables and applications. Boston, MA: McGraw-Hill Higher Education.
Use the Residue Theorem to evaluate the integral of

in the region 
Note,
Thus, seeking to apply the Residue Theorem above for 


Observe, the coefficient of 

Thus,
![\text{Res}_{z=0} [\frac{1}{z^2}f(\frac{1}{z})] = 2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067303/gif.latex)
Therefore, by the Residue Theorem above,
Hence,
Example Question #7 : Residue Theory
Cauchy's Residue Theorem is as follows:
Let 




For the following problem, use a modified version of the theorem which goes as follows:
Residue Theorem
If a function 

Brown, J. W., & Churchill, R. V. (2009). Complex variables and applications. Boston, MA: McGraw-Hill Higher Education.
Use the Residue Theorem to evaluate the integral of

in the region 
Note,
Thus, seeking to apply the Residue Theorem above for 


Observe,
The coefficient of 

Thus,
![\text{Res}_{z=0} [\frac{1}{z^2}f(\frac{1}{z})] = 7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067314/gif.latex)
Therefore, by the Residue Theorem above,
Hence,
Example Question #8 : Residue Theory
Find the residue of the function

Observe
The coefficient of 

Thus,
![\text{Res}_{z=0}[f(z)] = \text{Res}_{z=0}[\frac{cot(z)}{z^6}] = - \frac{2}{945}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067330/gif.latex)
Example Question #3 : Residue Theory
Find the residue at 

Let 
Observe,
The coefficient of 


Thus,
Example Question #51 : Complex Analysis
Find the residue at 

Observe,
The coefficient of 

Thus,
![\text{Res}_{z=0} [f(z)] = \text{Res}_{z=0} [\frac{4}{z+z^2}] = 4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067347/gif.latex)
Example Question #11 : Residue Theory
Find the residue at 

Observe,

The coefficient of 

Thus,
![\text{Res}_{z=0} [f(z)] = \text{Res}_{z=0} [\frac{z^2 - sin(z)}{z^2}] = -1](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067810/gif.latex)
Example Question #53 : Complex Analysis
If 


None of the other answers




Since 

Since 

Putting these two results together gives us
which implies that 



Certified Tutor
Certified Tutor
All Complex Analysis Resources


![\displaystyle\int_{C} f(z) dz = 2 \pi i \text{Res}_{z=0} [\frac{1}{z^2}f(\frac{1}{z})]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067162/gif.latex)






![\displaystyle \int_{|z|=3} f(z) dz = 2 \pi i \text{Res}_{z=0}[\frac{1}{z^2}f(\frac{1}{z})] = 2 \pi i (0) = 0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067289/gif.latex)

![\displaystyle\int_{C} f(z) dz = 2 \pi i \text{Res}_{z=0} [\frac{1}{z^2}f(\frac{1}{z})]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067146/gif.latex)







![\displaystyle \int_{|z|=3} f(z) dz = 2 \pi i \text{Res}_{z=0}[\frac{1}{z^2}f(\frac{1}{z})] = 2 \pi i (5) = 10 \pi i](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067281/gif.latex)

![\displaystyle\int_{C} f(z) dz = 2 \pi i \text{Res}_{z=0} [\frac{1}{z^2}f(\frac{1}{z})]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067176/gif.latex)







![\displaystyle \int_{|z|=2} f(z) dz = 2 \pi i \text{Res}_{z=0}[\frac{1}{z^2}f(\frac{1}{z})] = 2 \pi i (0) = 0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067219/gif.latex)







![\displaystyle \int_{|z|=2} f(z) dz = 2 \pi i \text{Res}_{z=0}[\frac{1}{z^2}f(\frac{1}{z})] = 2 \pi i (2) = 4 \pi i](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067304/gif.latex)








![\displaystyle \int_{|z|=2} f(z) dz = 2 \pi i \text{Res}_{z=0}[\frac{1}{z^2}f(\frac{1}{z})] = 2 \pi i (7) = 14 \pi i](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067315/gif.latex)













![\text{Res}_{z=0}[f(z))] = \text{Res}_{z=0}[z \cos (\frac{1}{z})] = 0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1067342/gif.latex)