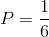All Common Core: High School - Statistics and Probability Resources
Example Questions
Example Question #11 : Describe Events As Subsets Of A Sample Space: Ccss.Math.Content.Hss Cp.A.1
Market analysts for an automotive company randomly sampled five hundred new car buyers using a simple survey. This survey recorded the preferences of future consumers. The analysts documented several preferences in the same survey: engine size (i.e. an eight cylinder—V8—or a six cylinder—V6) and paint color. The data are present in the provided table.
What of the following correctly calculates the probability intersection future consumers that will want a car that is Candy Apple Red and has a V8?
In order to solve this problem, we need to discuss probabilities. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now, we can discuss other terms related with probabilities. The complement of an event is the outcomes that do not include the event. In other words, what is the probability of not rolling one? For instance, in the previous example, we wanted to know the probability of rolling a one on a die. The complement of this event would be rolling everything but a one. The event in the complement would be rolling a two, three, four, five, or a six. We can calculate the probability using the following method:
Convert to a percentage
We can also find the complement by subtracting the probability of the event from the maximum probability value of one:
It is important to note that in this case the complement is more likely to occur than the original event.
Next, lets discuss unions and intersections. Regarding probabilities, a union is the likelihood that one event or another will occur. For instance, what is the probability that a person will role a one or a six on a die?
Convert to a percentage.
Last, an intersection is the likelihood that one event will occur with another. What is the probability that we will roll a one and flip a coin to reveal heads? We know that the probability of rolling a one is:
Now, let's determine the probability of flipping a coin to reveal the heads side. A coin has two sides: heads or tails. The probability of rolling heads is as follows:
An intersection is the probability of two events occurring simultaneously; therefore, we need to multiply the probabilities.
Convert to a percentage.
Let's look at a table that contains these specific probabilities and the key words that are indicative of each.

Now, let's use this question to solve the problem. The question asks us to find the probability of an intersection: cars that are Candy Apple Red with V8 engines.
Example Question #12 : Describe Events As Subsets Of A Sample Space: Ccss.Math.Content.Hss Cp.A.1
Market analysts for an automotive company randomly sampled five hundred new car buyers using a simple survey. This survey recorded the preferences of future consumers. The analysts documented several preferences in the same survey: engine size (i.e. an eight cylinder—V8—or a six cylinder—V6) and paint color. The data are present in the provided table.
What of the following correctly calculates the probability intersection future consumers that will want a car that is Candy Apple Red and has a V8?
In order to solve this problem, we need to discuss probabilities. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now, we can discuss other terms related with probabilities. The complement of an event is the outcomes that do not include the event. In other words, what is the probability of not rolling one? For instance, in the previous example, we wanted to know the probability of rolling a one on a die. The complement of this event would be rolling everything but a one. The event in the complement would be rolling a two, three, four, five, or a six. We can calculate the probability using the following method:
Convert to a percentage
We can also find the complement by subtracting the probability of the event from the maximum probability value of one:
It is important to note that in this case the complement is more likely to occur than the original event.
Next, lets discuss unions and intersections. Regarding probabilities, a union is the likelihood that one event or another will occur. For instance, what is the probability that a person will role a one or a six on a die?
Convert to a percentage.
Last, an intersection is the likelihood that one event will occur with another. What is the probability that we will roll a one and flip a coin to reveal heads? We know that the probability of rolling a one is:
Now, let's determine the probability of flipping a coin to reveal the heads side. A coin has two sides: heads or tails. The probability of rolling heads is as follows:
An intersection is the probability of two events occurring simultaneously; therefore, we need to multiply the probabilities.
Convert to a percentage.
Let's look at a table that contains these specific probabilities and the key words that are indicative of each.

Now, let's use this question to solve the problem. The question asks us to find the probability of an intersection: cars that are Candy Apple Red with V8 engines.
Example Question #13 : Describe Events As Subsets Of A Sample Space: Ccss.Math.Content.Hss Cp.A.1
Market analysts for an automotive company randomly sampled five hundred new car buyers using a simple survey. This survey recorded the preferences of future consumers. The analysts documented several preferences in the same survey: engine size (i.e. an eight cylinder—V8—or a six cylinder—V6) and paint color. The data are present in the provided table.
What of the following correctly calculates the probability intersection future consumers that will want a car that is Black Pearl and has a V8?
In order to solve this problem, we need to discuss probabilities. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now, we can discuss other terms related with probabilities. The complement of an event is the outcomes that do not include the event. In other words, what is the probability of not rolling one? For instance, in the previous example, we wanted to know the probability of rolling a one on a die. The complement of this event would be rolling everything but a one. The event in the complement would be rolling a two, three, four, five, or a six. We can calculate the probability using the following method:
Convert to a percentage
We can also find the complement by subtracting the probability of the event from the maximum probability value of one:
It is important to note that in this case the complement is more likely to occur than the original event.
Next, lets discuss unions and intersections. Regarding probabilities, a union is the likelihood that one event or another will occur. For instance, what is the probability that a person will role a one or a six on a die?
Convert to a percentage.
Last, an intersection is the likelihood that one event will occur with another. What is the probability that we will roll a one and flip a coin to reveal heads? We know that the probability of rolling a one is:
Now, let's determine the probability of flipping a coin to reveal the heads side. A coin has two sides: heads or tails. The probability of rolling heads is as follows:
An intersection is the probability of two events occurring simultaneously; therefore, we need to multiply the probabilities.
Convert to a percentage.
Let's look at a table that contains these specific probabilities and the key words that are indicative of each.

Now, let's use this question to solve the problem. The question asks us to find the probability of an intersection: cars that are Black Pearl with V8 engines.

Example Question #14 : Describe Events As Subsets Of A Sample Space: Ccss.Math.Content.Hss Cp.A.1
Market analysts for an automotive company randomly sampled five hundred new car buyers using a simple survey. This survey recorded the preferences of future consumers. The analysts documented several preferences in the same survey: engine size (i.e. an eight cylinder—V8—or a six cylinder—V6) and paint color. The data are present in the provided table.
What of the following correctly calculates the probability intersection future consumers that will want a car that is Candy Apple Red and has a V8?
In order to solve this problem, we need to discuss probabilities. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now, we can discuss other terms related with probabilities. The complement of an event is the outcomes that do not include the event. In other words, what is the probability of not rolling one? For instance, in the previous example, we wanted to know the probability of rolling a one on a die. The complement of this event would be rolling everything but a one. The event in the complement would be rolling a two, three, four, five, or a six. We can calculate the probability using the following method:
Convert to a percentage
We can also find the complement by subtracting the probability of the event from the maximum probability value of one:
It is important to note that in this case the complement is more likely to occur than the original event.
Next, lets discuss unions and intersections. Regarding probabilities, a union is the likelihood that one event or another will occur. For instance, what is the probability that a person will role a one or a six on a die?
Convert to a percentage.
Last, an intersection is the likelihood that one event will occur with another. What is the probability that we will roll a one and flip a coin to reveal heads? We know that the probability of rolling a one is:
Now, let's determine the probability of flipping a coin to reveal the heads side. A coin has two sides: heads or tails. The probability of rolling heads is as follows:
An intersection is the probability of two events occurring simultaneously; therefore, we need to multiply the probabilities.
Convert to a percentage.
Let's look at a table that contains these specific probabilities and the key words that are indicative of each.

Now, let's use this question to solve the problem. The question asks us to find the probability of an intersection: cars that are Candy Apple Red with V8 engines.
Example Question #11 : Conditional Probability & The Rules Of Probability
There is a 25% chance of rain tomorrow. The probability that the price of gold rises tomorrow is 37%. The probability that it rains AND the price of gold rises tomorrow is 9.25%. Are the two events independent?
yes
cannot be determined
no
yes
Example Question #12 : Conditional Probability & The Rules Of Probability
A car dealership takes its automotive inventory. They decide to note the number of cars and trucks are in the lot as well as the type of transmission the vehicles have: automatic or manual. They input this data into the following table:

A potential car buyer wants to purchase a vehicle and inquires if vehicle type is independent of transmission style. According to the data, is purchasing a truck independent of it possessing a manual transmission?
In order to solve problems associated with this standard, we need to understand two primary components: probabilities and the property of independent events. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we can calculate a probability, we can review the property of independent events. The probability of independent events states that two events (A and B) are independent if and only if the probability of event A times the probability of event B equals the probability of the intersection of both events A and B occurring. It can be written as the following expression:
Let's return to the dice example. Is the probability of rolling a one on one die independent to rolling a two on a separate die on the same roll? First, let's calculate the probability of rolling a one.
Now, let's find the probability of rolling a two on a separate die in the same roll.
Let's multiply these two probabilities together.
Now, let's find the probability of rolling both a one and a two in the same roll on two separate dice.
Let's compare the two probabilities.
The probabilities are equal, therefore,
Let's look at another example. A person has a bag full of ten marbles: six white and four black marbles. He wants to know if the probability of pulling out a white marble is independent of pulling out a black marble. Let's start by calculating the probability of pulling out a black marble.
Now let's calculate the probability of pulling out a white marble.
Let's multiply these two probabilities together.
Now let's observe these events occurring at simultaneously. Let's say that a black marble is pulled out of the bag first. The probability of the black marble is as follows:
It is the same as before; however, the probability of pulling out a white marble has changed because one marble has been removed from the bag.
The probability of both occurring can be written as the following:
The probabilities are not equal.
This is because these two events are dependent on one another. When a marble is pulled on the first grab (whether it is black or white) and not replaced, there is a different total number of marbles to be pulled on the second grab. As a result, the probability of pulling a marble of a specific color changes from the initial event to the second event. This scenario could be made independent by either using two separate bags with the same marble composition or by replacing the marbles after they are pulled before pulling another one on a second try. This information has ilustrated the property of independence and how to calculate if events are independent from one another.
Now, we can use this information to solve the problem. The question asks us to determine if the probability of buying a truck is independent of it having manual transmission. In this case, we need to investigate whether or not the following expression is true:
First, let's calculate the probability associated with finding a truck in the lot.
Now let's calculate the probability of a vehicle having a manual transmission.
Now, we need to calculate the probability of both of these events occurring simultaneously.
Now, let's find out if the following expression is true:
Using this information, we know that the correct answer is the following:
Example Question #12 : Conditional Probability & The Rules Of Probability
A car dealership takes its automotive inventory. They decide to note the number of cars and trucks are in the lot as well as the type of transmission the vehicles have: automatic or manual. They input this data into the following table:
A potential car buyer wants to purchase a vehicle and inquires if vehicle type is independent of transmission style. According to the data, is purchasing a, car independent of it possessing a automatic transmission?
In order to solve problems associated with this standard, we need to understand two primary components: probabilities and the property of independent events. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we can calculate a probability, we can review the property of independent events. The probability of independent events states that two events (A and B) are independent if and only if the probability of event A times the probability of event B equals the probability of the intersection of both events A and B occurring. It can be written as the following expression:
Let's return to the dice example. Is the probability of rolling a one on one die independent to rolling a two on a separate die on the same roll? First, let's calculate the probability of rolling a one.
Now, let's find the probability of rolling a two on a separate die in the same roll.
Let's multiply these two probabilities together.
Now, let's find the probability of rolling both a one and a two in the same roll on two separate dice.
Let's compare the two probabilities.
The probabilities are equal, therefore,
Let's look at another example. A person has a bag full of ten marbles: six white and four black marbles. He wants to know if the probability of pulling out a white marble is independent of pulling out a black marble. Let's start by calculating the probability of pulling out a black marble.
Now let's calculate the probability of pulling out a white marble.
Let's multiply these two probabilities together.
Now let's observe these events occurring at simultaneously. Let's say that a black marble is pulled out of the bag first. The probability of the black marble is as follows:
It is the same as before; however, the probability of pulling out a white marble has changed because one marble has been removed from the bag.
The probability of both occurring can be written as the following:
The probabilities are not equal.
This is because these two events are dependent on one another. When a marble is pulled on the first grab (whether it is black or white) and not replaced, there is a different total number of marbles to be pulled on the second grab. As a result, the probability of pulling a marble of a specific color changes from the initial event to the second event. This scenario could be made independent by either using two separate bags with the same marble composition or by replacing the marbles after they are pulled before pulling another one on a second try. This information has ilustrated the property of independence and how to calculate if events are independent from one another.
Now, we can use this information to solve the problem. The question asks us to determine if the probability of buying a truck is independent of it having manual transmission. In this case, we need to investigate whether or not the following expression is true:
First, let's calculate the probability associated with finding a car in the lot.
Now let's calculate the probability of a vehicle having a automatic transmission.
Now, we need to calculate the probability of both of these events occurring simultaneously.
Now, let's find out if the following expression is true:
Using this information, we know that the correct answer is the following:
Example Question #18 : Conditional Probability & The Rules Of Probability
A car dealership takes its automotive inventory. They decide to note the number of cars and trucks are in the lot as well as the type of transmission the vehicles have: automatic or manual. They input this data into the following table:
A potential car buyer wants to purchase a vehicle and inquires if vehicle type is independent of transmission style. According to the data, is purchasing a, car independent of it possessing a automatic transmission?
In order to solve problems associated with this standard, we need to understand two primary components: probabilities and the property of independent events. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we can calculate a probability, we can review the property of independent events. The probability of independent events states that two events (A and B) are independent if and only if the probability of event A times the probability of event B equals the probability of the intersection of both events A and B occurring. It can be written as the following expression:
Let's return to the dice example. Is the probability of rolling a one on one die independent to rolling a two on a separate die on the same roll? First, let's calculate the probability of rolling a one.
Now, let's find the probability of rolling a two on a separate die in the same roll.
Let's multiply these two probabilities together.
Now, let's find the probability of rolling both a one and a two in the same roll on two separate dice.
Let's compare the two probabilities.
The probabilities are equal, therefore,
Let's look at another example. A person has a bag full of ten marbles: six white and four black marbles. He wants to know if the probability of pulling out a white marble is independent of pulling out a black marble. Let's start by calculating the probability of pulling out a black marble.
Now let's calculate the probability of pulling out a white marble.
Let's multiply these two probabilities together.
Now let's observe these events occurring at simultaneously. Let's say that a black marble is pulled out of the bag first. The probability of the black marble is as follows:
It is the same as before; however, the probability of pulling out a white marble has changed because one marble has been removed from the bag.
The probability of both occurring can be written as the following:
The probabilities are not equal.
This is because these two events are dependent on one another. When a marble is pulled on the first grab (whether it is black or white) and not replaced, there is a different total number of marbles to be pulled on the second grab. As a result, the probability of pulling a marble of a specific color changes from the initial event to the second event. This scenario could be made independent by either using two separate bags with the same marble composition or by replacing the marbles after they are pulled before pulling another one on a second try. This information has ilustrated the property of independence and how to calculate if events are independent from one another.
Now, we can use this information to solve the problem. The question asks us to determine if the probability of buying a truck is independent of it having manual transmission. In this case, we need to investigate whether or not the following expression is true:
First, let's calculate the probability associated with finding a car in the lot.
Now let's calculate the probability of a vehicle having a automatic transmission.
Now, we need to calculate the probability of both of these events occurring simultaneously.
Now, let's find out if the following expression is true:
Using this information, we know that the correct answer is the following:
Example Question #19 : Conditional Probability & The Rules Of Probability
A car dealership takes its automotive inventory. They decide to note the number of cars and trucks are in the lot as well as the type of transmission the vehicles have: automatic or manual. They input this data into the following table:
A potential car buyer wants to purchase a vehicle and inquires if vehicle type is independent of transmission style. According to the data, is purchasing a, car independent of it possessing a automatic transmission?
In order to solve problems associated with this standard, we need to understand two primary components: probabilities and the property of independent events. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we can calculate a probability, we can review the property of independent events. The probability of independent events states that two events (A and B) are independent if and only if the probability of event A times the probability of event B equals the probability of the intersection of both events A and B occurring. It can be written as the following expression:
Let's return to the dice example. Is the probability of rolling a one on one die independent to rolling a two on a separate die on the same roll? First, let's calculate the probability of rolling a one.
Now, let's find the probability of rolling a two on a separate die in the same roll.
Let's multiply these two probabilities together.
Now, let's find the probability of rolling both a one and a two in the same roll on two separate dice.
Let's compare the two probabilities.
The probabilities are equal, therefore,
Let's look at another example. A person has a bag full of ten marbles: six white and four black marbles. He wants to know if the probability of pulling out a white marble is independent of pulling out a black marble. Let's start by calculating the probability of pulling out a black marble.
Now let's calculate the probability of pulling out a white marble.
Let's multiply these two probabilities together.
Now let's observe these events occurring at simultaneously. Let's say that a black marble is pulled out of the bag first. The probability of the black marble is as follows:
It is the same as before; however, the probability of pulling out a white marble has changed because one marble has been removed from the bag.
The probability of both occurring can be written as the following:
The probabilities are not equal.
This is because these two events are dependent on one another. When a marble is pulled on the first grab (whether it is black or white) and not replaced, there is a different total number of marbles to be pulled on the second grab. As a result, the probability of pulling a marble of a specific color changes from the initial event to the second event. This scenario could be made independent by either using two separate bags with the same marble composition or by replacing the marbles after they are pulled before pulling another one on a second try. This information has ilustrated the property of independence and how to calculate if events are independent from one another.
Now, we can use this information to solve the problem. The question asks us to determine if the probability of buying a truck is independent of it having manual transmission. In this case, we need to investigate whether or not the following expression is true:
First, let's calculate the probability associated with finding a car in the lot.
Now let's calculate the probability of a vehicle having a automatic transmission.
Now, we need to calculate the probability of both of these events occurring simultaneously.
Now, let's find out if the following expression is true:
Using this information, we know that the correct answer is the following:
Example Question #20 : Conditional Probability & The Rules Of Probability
A car dealership takes its automotive inventory. They decide to note the number of cars and trucks are in the lot as well as the type of transmission the vehicles have: automatic or manual. They input this data into the following table:
A potential car buyer wants to purchase a vehicle and inquires if vehicle type is independent of transmission style. According to the data, is purchasing a, car independent of it possessing a automatic transmission?
In order to solve problems associated with this standard, we need to understand two primary components: probabilities and the property of independent events. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we can calculate a probability, we can review the property of independent events. The probability of independent events states that two events (A and B) are independent if and only if the probability of event A times the probability of event B equals the probability of the intersection of both events A and B occurring. It can be written as the following expression:
Let's return to the dice example. Is the probability of rolling a one on one die independent to rolling a two on a separate die on the same roll? First, let's calculate the probability of rolling a one.
Now, let's find the probability of rolling a two on a separate die in the same roll.
Let's multiply these two probabilities together.
Now, let's find the probability of rolling both a one and a two in the same roll on two separate dice.
Let's compare the two probabilities.
The probabilities are equal, therefore,
Let's look at another example. A person has a bag full of ten marbles: six white and four black marbles. He wants to know if the probability of pulling out a white marble is independent of pulling out a black marble. Let's start by calculating the probability of pulling out a black marble.
Now let's calculate the probability of pulling out a white marble.
Let's multiply these two probabilities together.
Now let's observe these events occurring at simultaneously. Let's say that a black marble is pulled out of the bag first. The probability of the black marble is as follows:
It is the same as before; however, the probability of pulling out a white marble has changed because one marble has been removed from the bag.
The probability of both occurring can be written as the following:
The probabilities are not equal.
This is because these two events are dependent on one another. When a marble is pulled on the first grab (whether it is black or white) and not replaced, there is a different total number of marbles to be pulled on the second grab. As a result, the probability of pulling a marble of a specific color changes from the initial event to the second event. This scenario could be made independent by either using two separate bags with the same marble composition or by replacing the marbles after they are pulled before pulling another one on a second try. This information has ilustrated the property of independence and how to calculate if events are independent from one another.
Now, we can use this information to solve the problem. The question asks us to determine if the probability of buying a truck is independent of it having manual transmission. In this case, we need to investigate whether or not the following expression is true:
First, let's calculate the probability associated with finding a car in the lot.
Now let's calculate the probability of a vehicle having a automatic transmission.
Now, we need to calculate the probability of both of these events occurring simultaneously.
Now, let's find out if the following expression is true:
Using this information, we know that the correct answer is the following:
All Common Core: High School - Statistics and Probability Resources