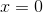This question is testing one's ability to analyze a function algebraically and graphically and identify the vertex of a function. Identifying properties of functions through analyzing equivalent forms is critical to this concept. Such properties that can be found through analyzing the different forms of a function include finding roots (zeros), extreme values, symmetry, and intercepts. 

For the purpose of Common Core Standards, finding the line of symmetry falls within the Cluster C of analyze functions using different representations concept (CCSS.MATH.CONTENT.HSF-IF.C.8). 

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Use technology to graph the function.

Step 2: Recognize the formula for calculating the vertex of a parabola.

The  coordinate of the vertex can be found using the following formula.

Substituting in the values for this particular function results in the following.

Step 3: Verify by graphing that the  value in the function's vertex represents the line of symmetry.

Therefore, the line of symmetry occurs at .

This question is testing one's ability to analyze a function algebraically and recognize different but equivalent forms. Identifying properties of functions through analyzing equivalent forms is critical to this concept. Such properties that can be found through analyzing the different forms of a function include finding roots (zeros), extreme values, symmetry, and intercepts.

For the purpose of Common Core Standards, factoring by way of completing the square falls within the Cluster C of analyze functions using different representations concept (CCSS.Math.content.HSF-IF.C.8). 

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

When it comes to finding equivalent forms of quadratics, there are two main approaches.

   I. Factoring

   II. Completing the square

This particular question wants the question to be solved using method II. completing the square. It is important to recall that the zeros of a function are areas where the graph crosses the -axis. In other words, finding the roots of a function is to find which  values result in  equalling zero. 

For this particular problem the steps are as follows.

Step 1: Identify mathematically how completing the square works.

Given a function,

Divide the  term by two, then square it and add it to both sides of the equation.

Assuming ,

Then the factored form becomes,

Recall that  are constants.

Step 2: Solve for .

Apply the above steps to this particular problem to solve.

Step 1: Identify mathematically how completing the square works.

Simplifying results in,

Then the factored form becomes,

Step 2: Solve for .

Step 3: Verify results and check for extraneous solutions.

Use opposite operations to move the constants from one side to the other.

Step 3: Verify results.

To verify that these two values are the roots of the function, substitute them in for  in the original function. If they result in zero as the output value then they are in fact a zero (root). When both values are substituted into the function and solved using a calculator it is seen that both values result in a root.