All Common Core: 8th Grade Math Resources
Example Questions
Example Question #7 : Understand Congruency Of Two Dimensional Figures: Ccss.Math.Content.8.G.A.2
Are the two shapes shown in the coordinate plane congruent? If so, what transformation did the red shape undergo from the orange shape?

Yes, refection over the x-axis
Yes, translation down
No
Yes, 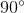
No
In order to solve this problem, we first need to know what "congruent" means. For two shapes to be congruent, they need to be the same shape and the same size. The shape can go through a transformation—rotation, translation, or reflection—but nothing else about the original shape can be changed for two shapes to be congruent.
Also, let's recall the types of transformations:
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
For this question, we can tell that the triangles are not the same size, the red triangle is narrower; thus, the triangles are not congruent.
Example Question #361 : Grade 8
Are the two shapes shown in the coordinate plane congruent? If so, what transformation did the red shape undergo from the orange shape?

No
Yes, translation down
Yes, refection over the x-axis
Yes, 
No
In order to solve this problem, we first need to know what "congruent" means. For two shapes to be congruent, they need to be the same shape and the same size. The shape can go through a transformation—rotation, translation, or reflection—but nothing else about the original shape can be changed for two shapes to be congruent.
Also, let's recall the types of transformations:
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
For this question, we can tell that the triangles are not the same size, the red triangle is narrower; thus, the triangles are not congruent.
Example Question #12 : Understand Congruency Of Two Dimensional Figures: Ccss.Math.Content.8.G.A.2
Are the two shapes shown in the coordinate plane congruent? If so, what transformation did the red shape undergo from the orange shape?

Yes, 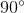
No
Yes, refection over the x-axis
Yes, translation down and to the left
No
In order to solve this problem, we first need to know what "congruent" means. For two shapes to be congruent, they need to be the same shape and the same size. The shape can go through a transformation—rotation, translation, or reflection—but nothing else about the original shape can be changed for two shapes to be congruent.
Also, let's recall the types of transformations:
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
For this question, we can tell that the triangles are not the same size, the red triangle is narrower; thus, the triangles are not congruent.
Example Question #42 : Geometry
What is the scale of the dilation that the blue rectangle underwent to get the purple rectangle in the image provided?

A dilation creates an image of the same shape, but of a different size. Dilations are always done with a certain scale factor. Let's look at the image in the picture and determine the length and width of each of the rectangles:

Notice that both the length and the width of the rectangle doubles in the purple rectangle, from the blue rectangle; thus the scale of the dilation is
Example Question #44 : Geometry
What is the scale of the dilation that the blue rectangle underwent to get the purple rectangle in the image provided?

A dilation creates an image of the same shape, but of a different size. Dilations are always done with a certain scale factor. Let's look at the image in the picture and determine the length and width of each of the rectangles:

Notice that both the length and the width of the rectangle triples in the purple rectangle, from the blue rectangle; thus the scale of the dilation is
Example Question #51 : Geometry
What is the scale of the dilation that the blue rectangle underwent to get the purple rectangle in the image provided?

A dilation creates an image of the same shape, but of a different size. Dilations are always done with a certain scale factor. Let's look at the image in the picture and determine the length and width of each of the rectangles:

Notice that both the length and the width of the rectangle is half in the purple rectangle, from the blue rectangle; thus the scale of the dilation is
Example Question #52 : Geometry
What is the scale of the dilation that the blue rectangle underwent to get the purple rectangle in the image provided?

A dilation creates an image of the same shape, but of a different size. Dilations are always done with a certain scale factor. Let's look at the image in the picture and determine the length and width of each of the rectangles:

Notice that both the length and the width of the rectangle doubles in the purple rectangle, from the blue rectangle; thus the scale of the dilation is
Example Question #53 : Geometry
What is the scale of the dilation that the blue rectangle underwent to get the purple rectangle in the image provided?

A dilation creates an image of the same shape, but of a different size. Dilations are always done with a certain scale factor. Let's look at the image in the picture and determine the length and width of each of the rectangles:

Notice that both the length and the width of the rectangle triples in the purple rectangle, from the blue rectangle; thus the scale of the dilation is
Example Question #54 : Geometry
What is the scale of the dilation that the blue rectangle underwent to get the purple rectangle in the image provided?

A dilation creates an image of the same shape, but of a different size. Dilations are always done with a certain scale factor. Let's look at the image in the picture and determine the length and width of each of the rectangles:

Notice that both the length and the width of the rectangle quadrupled in the purple rectangle, from the blue rectangle; thus the scale of the dilation is
Example Question #55 : Geometry
What is the scale of the dilation that the blue rectangle underwent to get the purple rectangle in the image provided?

A dilation creates an image of the same shape, but of a different size. Dilations are always done with a certain scale factor. Let's look at the image in the picture and determine the length and width of each of the rectangles:

Notice that both the length and the width of the rectangle doubles in the purple rectangle, from the blue rectangle; thus the scale of the dilation is
Certified Tutor
Certified Tutor
All Common Core: 8th Grade Math Resources














































