All Common Core: 8th Grade Math Resources
Example Questions
Example Question #4 : Use Informal Arguments To Establish Facts About The Angle Sum And Exterior Angle Of Triangles: Ccss.Math.Content.8.G.A.5
The image provided contains a set of parallel lines, 




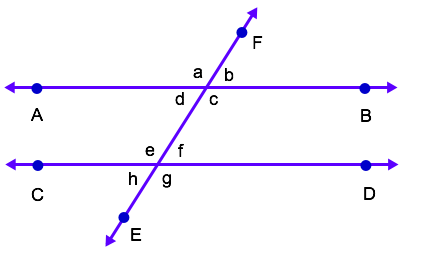
First, we need to define some key terms:
Parallel Lines: Parallel lines are lines that will never intersect with each other.
Transversal Line: A transversal line is a line that crosses two parallel lines.
In the the image provided, lines 


It is important to know that transversal lines create angle relationships:
- Vertical angles are congruent
- Corresponding angles are congruent
- Alternate interior angles are congruent
- Alternate exterior angles are congruent
Let's look at angle 

Angle 

Angle 

Angle 

Angle 




For this problem, we want to find the angle that is congruent to angle 




Example Question #5 : Use Informal Arguments To Establish Facts About The Angle Sum And Exterior Angle Of Triangles: Ccss.Math.Content.8.G.A.5
The image provided contains a set of parallel lines, 





First, we need to define some key terms:
Parallel Lines: Parallel lines are lines that will never intersect with each other.
Transversal Line: A transversal line is a line that crosses two parallel lines.
In the the image provided, lines 


It is important to know that transversal lines create angle relationships:
- Vertical angles are congruent
- Corresponding angles are congruent
- Alternate interior angles are congruent
- Alternate exterior angles are congruent
Let's look at angle 

Angle 

Angle 

Angle 

Angle 




For this problem, we want to find the angle that is congruent to angle 




Example Question #6 : Use Informal Arguments To Establish Facts About The Angle Sum And Exterior Angle Of Triangles: Ccss.Math.Content.8.G.A.5
The image provided contains a set of parallel lines, 





First, we need to define some key terms:
Parallel Lines: Parallel lines are lines that will never intersect with each other.
Transversal Line: A transversal line is a line that crosses two parallel lines.
In the the image provided, lines 


It is important to know that transversal lines create angle relationships:
- Vertical angles are congruent
- Corresponding angles are congruent
- Alternate interior angles are congruent
- Alternate exterior angles are congruent
Let's look at angle 

Angle 

Angle 

Angle 

Angle 




For this problem, we want to find the angle that is congruent to angle 




Example Question #7 : Use Informal Arguments To Establish Facts About The Angle Sum And Exterior Angle Of Triangles: Ccss.Math.Content.8.G.A.5
The image provided contains a set of parallel lines, 





First, we need to define some key terms:
Parallel Lines: Parallel lines are lines that will never intersect with each other.
Transversal Line: A transversal line is a line that crosses two parallel lines.
In the the image provided, lines 


It is important to know that transversal lines create angle relationships:
- Vertical angles are congruent
- Corresponding angles are congruent
- Alternate interior angles are congruent
- Alternate exterior angles are congruent
Let's look at angle 

Angle 

Angle 

Angle 

Angle 




For this problem, we want to find the angle that is congruent to angle 




Example Question #8 : Use Informal Arguments To Establish Facts About The Angle Sum And Exterior Angle Of Triangles: Ccss.Math.Content.8.G.A.5
The image provided contains a set of parallel lines, 



First, we need to define some key terms:
Parallel Lines: Parallel lines are lines that will never intersect with each other.
Transversal Line: A transversal line is a line that crosses two parallel lines.
In the the image provided, lines 


It is important to know that transversal lines create angle relationships:
- Vertical angles are congruent
- Corresponding angles are congruent
- Alternate interior angles are congruent
- Alternate exterior angles are congruent
Let's look at angle 

Angle 

Angle 

Angle 

Angle 




For this problem, we want to find the angle that is not equal to to angle 
Angle 

Angle 

Angle 

However, angle 

Example Question #9 : Use Informal Arguments To Establish Facts About The Angle Sum And Exterior Angle Of Triangles: Ccss.Math.Content.8.G.A.5
The image provided contains a set of parallel lines, 



First, we need to define some key terms:
Parallel Lines: Parallel lines are lines that will never intersect with each other.
Transversal Line: A transversal line is a line that crosses two parallel lines.
In the the image provided, lines 


It is important to know that transversal lines create angle relationships:
- Vertical angles are congruent
- Corresponding angles are congruent
- Alternate interior angles are congruent
- Alternate exterior angles are congruent
Let's look at angle 

Angle 

Angle 

Angle 

Angle 




For this problem, we want to find the angle that is not equal to to angle 
Angle 

Angle 

Angle 

However, angle 

Example Question #10 : Use Informal Arguments To Establish Facts About The Angle Sum And Exterior Angle Of Triangles: Ccss.Math.Content.8.G.A.5
The image provided contains a set of parallel lines, 



First, we need to define some key terms:
Parallel Lines: Parallel lines are lines that will never intersect with each other.
Transversal Line: A transversal line is a line that crosses two parallel lines.
In the the image provided, lines 


It is important to know that transversal lines create angle relationships:
- Vertical angles are congruent
- Corresponding angles are congruent
- Alternate interior angles are congruent
- Alternate exterior angles are congruent
Let's look at angle 

Angle 

Angle 

Angle 

Angle 




For this problem, we want to find the angle that is not equal to to angle 
Angle 

Angle 

Angle 

However, angle 

Example Question #11 : Use Informal Arguments To Establish Facts About The Angle Sum And Exterior Angle Of Triangles: Ccss.Math.Content.8.G.A.5
The image provided contains a set of parallel lines, 



First, we need to define some key terms:
Parallel Lines: Parallel lines are lines that will never intersect with each other.
Transversal Line: A transversal line is a line that crosses two parallel lines.
In the the image provided, lines 


It is important to know that transversal lines create angle relationships:
- Vertical angles are congruent
- Corresponding angles are congruent
- Alternate interior angles are congruent
- Alternate exterior angles are congruent
Let's look at angle 

Angle 

Angle 

Angle 

Angle 




For this problem, we want to find the angle that is not equal to to angle 
Angle 

Angle 

Angle 

However, angle 

Example Question #391 : Grade 8
The image provided contains a set of parallel lines, 






First, we need to define some key terms:
Parallel Lines: Parallel lines are lines that will never intersect with each other.
Transversal Line: A transversal line is a line that crosses two parallel lines.
In the the image provided, lines 


It is important to know that transversal lines create angle relationships:
- Vertical angles are congruent
- Corresponding angles are congruent
- Alternate interior angles are congruent
- Alternate exterior angles are congruent
Let's look at angle 

Angle 

Angle 

Angle 

Angle 




For this problem, we want to find the angle that is congruent to angle 




Example Question #81 : Geometry
Which shape does the Pythagorean Theorem apply to?
Right triangles
Cubes
Triangles
Squares
Right triangles
The Pythagorean Theorem applies to right triangles. The Theorem states that for all right triangles, the square of the hypotenuse is equal to the sum of the square of the other two sides. In other terms:

All Common Core: 8th Grade Math Resources



















































