All College Algebra Resources
Example Questions
Example Question #31 : Zeros/Roots Of A Polynomial
Example Question #34 : Zeros/Roots Of A Polynomial
Example Question #35 : Zeros/Roots Of A Polynomial
Example Question #36 : Zeros/Roots Of A Polynomial
Example Question #37 : Zeros/Roots Of A Polynomial
Consider the polynomial
Which of the following is true of the rational zeroes of 
Hint: Think "Rational Zeroes Theorem".

1 is the only rational zero.
There are no rational zeroes.
Neither 

1 is the only rational zero.
By the Rational Zeroes Theorem, any rational zeroes of a polynomial must be obtainable by dividing a factor of the constant coefficient by a factor of the leading coefficient. Since both values are equal to 1, and 1 has only 1 as a factor, this restricts the set of possible rational zeroes to the set 
1 is a zero of 


1 is a zero.





1 is the only rational zero.
Example Question #38 : Zeros/Roots Of A Polynomial
The polynomial
has a zero on one of the following intervals. Which one?
The Intermediate value Theorem states that if 




![c \in [a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/966866/gif.latex)



for 

By substitution, we can find that:
The change in sign occurs on the interval 

Example Question #39 : Zeros/Roots Of A Polynomial
Consider the polynomial

The Rational Zeroes Theorem allows us to reduce the possible rational zeroes of this polynomial to a set comprising how many elements?
By the Rational Zeroes Theorem, any rational zero of a polynomial with integer coefficients must be equal to a factor of the constant divided by a factor of the leading coefficient, taking both positive and negative numbers into account.
The constant 17, being prime, has only two factors, 1 and 17; the leading coefficient is 1, which only has 1 as a factor. Thus, the only possible rational zeroes of the given polynomial are given in the set

a set of four elements. This makes 4 the correct choice.
Example Question #231 : College Algebra
Consider the polynomial

Going by Descartes' Rule of Signs alone, how many positive real zeroes could the polynomial have?
Exactly one
Exactly two
Exactly three
One or three
None or two
None or two
By Descartes' Rule of Signs, the number of positive real zeroes of a polynomial 
This means that this polynomial must have either zero or two such zeroes.
Example Question #231 : College Algebra
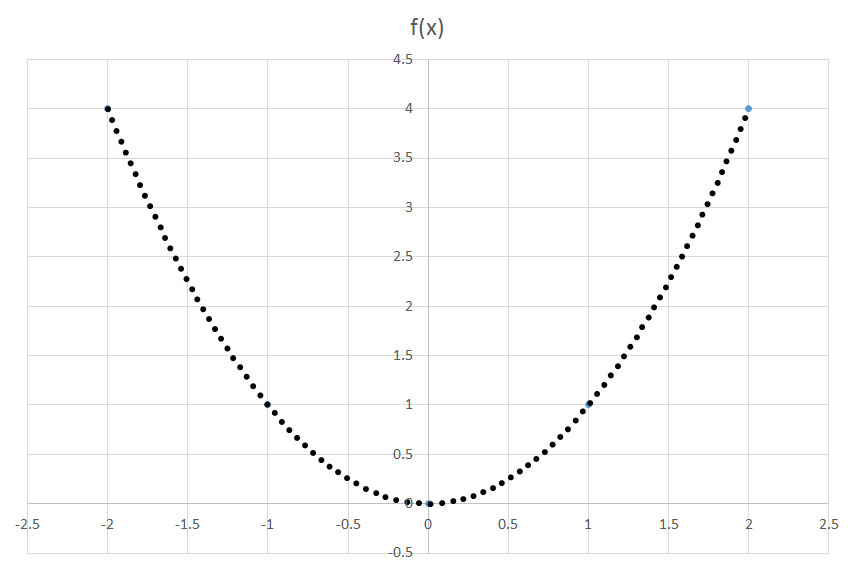
If the function 

Example Question #232 : College Algebra
Which of the following graphs correctly represents the quadratic inequality below (solutions to the inequalities are shaded in blue)?






To begin, we analyze the equation given: the base equation, 


To solve the inequality, we need to take a test point and plug it in to see if it matches the inequality. The only points that cannot be used are those directly on our parabola, so let's use the origin 
Simplified as:
Which is not true, so the area inside of the parabola should be shaded, resulting in the following graph:

Certified Tutor
All College Algebra Resources




















































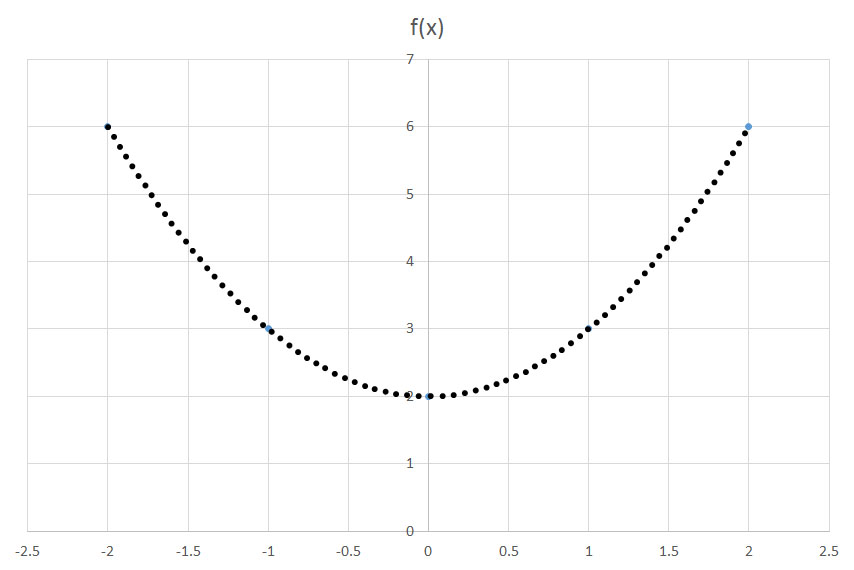
 shifts a function f(x)
shifts a function f(x)  units to the left. Conversely,
units to the left. Conversely,  shifts a function f(x)
shifts a function f(x)  units to the right. In this question, we are translating the graph two units to the left.
units to the right. In this question, we are translating the graph two units to the left. or
or  .
.





