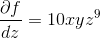All Calculus 3 Resources
Example Questions
Example Question #381 : Partial Derivatives
Find if , and .
Find if , and .
Keep in mind, when taking the derivative with respect to , is treated as a constant, and when taking the derivative with respect to , is treated as a constant.
To put solely in terms of and , we substitute the definitions of and given in the question, and .
Example Question #382 : Partial Derivatives
Find if , and .
Find if , and .
Keep in mind, when taking the derivative with respect to , is treated as a constant, and when taking the derivative with respect to , is treated as a constant.
To put solely in terms of and , we substitute the definitions of and given in the question, and .
Example Question #381 : Partial Derivatives
Find if , and .
Find if , and .
Keep in mind, when taking the derivative with respect to , is treated as a constant, and when taking the derivative with respect to , is treated as a constant.
To put solely in terms of and , we substitute the definitions of and given in the question, and .
Example Question #384 : Partial Derivatives
Find if , and .
Find if , and .
Keep in mind, when taking the derivative with respect to , is treated as a constant, and when taking the derivative with respect to , is treated as a constant.
To put solely in terms of and , we substitute the definitions of and given in the question, and .
Example Question #31 : Multi Variable Chain Rule
Find if , and .
Find if , and .
Keep in mind, when taking the derivative with respect to , is treated as a constant, and when taking the derivative with respect to , is treated as a constant.
To put solely in terms of and , we substitute the definitions of and given in the question, and .
Example Question #32 : Multi Variable Chain Rule
Find if , and .
Find if , and .
Keep in mind, when taking the derivative with respect to , is treated as a constant, and when taking the derivative with respect to , is treated as a constant.
To put solely in terms of and , we substitute the definitions of and given in the question, and .
Example Question #33 : Multi Variable Chain Rule
Compute for the function where the variables , and are functions of the of the parameter :
Compute for the function where the variables , and are functions of the of the parameter :
Because each function is given in terms of the parameter we can conveniently write the function as a function of alone:
Solution 1
For the function described in this problem, the function can be written strictly in terms of the parameter by simply substituting the definitions given for , or .
So now we have the function written in the form of a single variable function of We can use the usual chain-rule.
Apply the product rule and and the chain-rule:
Solution 2
The derivative of with respect to will be the sum of the derivatives of each variable , , and with respect to
(1)
In Equation (1) we use the partial derivative notation for a derivative of with respect to the variables , , and since it is a multi-variable function, we have to specify which variable we are differentiating unless we are differentiating with respect to
We return to the standard derivative notation when computing the derivatives with respect to since each function , , , and can be written as a single variable function of Now simply apply (3) to the function term-by-term:
Now ad the terms to get an expression for and then rewrite in terms of
Therefore:
Example Question #34 : Multi Variable Chain Rule
Find the two variable function that satisfies the following:
The first step is to integrate the function with respect to since that is the outer most derivative in this problem.
Now apply the constraints to compute the two constants of integration.
So far we have:
Now apply the second constraint given:
Example Question #381 : Partial Derivatives
Find .
In order to find , we need to take the derivative of in respect to , and treat , and as constants. We also need to remember what the derivatives of natural log, exponential functions and power functions are for single variables.
Natural Log:
Exponential Functions:
Power Functions:
Example Question #381 : Partial Derivatives
Find .
In order to find , we need to take the derivative of in respect to , and treat , and as constants. We also need to remember what the derivatives of natural log, exponential functions and power functions are for single variables.
Natural Log:
Exponential Functions:
Power Functions:
All Calculus 3 Resources
























![\frac{dz}{dt}=\left [ (2t-3)cos\left [ (-t^5+4t)(2t-3) \right ] \right ](-5t^4+4) +\left [ (-t^5+4t)cos\left [ (-t^5+4t)(2t-3) \right ] \right ](2)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/896795/gif.latex)
![\frac{dz}{dt}=\left [ (2t-3)(-5t^4+4)cos\left [ (-2t^6+8t^2+3t^5-12t) \right ] \right ] +\left [ 2(-t^5+4t)cos\left [ (-2t^6+8t^2+3t^5-12t) \right ] \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/896796/gif.latex)







![ln[sin(t)]sin(t)-\frac{cos^2(t)}{sin(t)}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/898116/gif.latex)
![ln[cos(t)]cos(t)-\frac{sin^2(t)}{cos(t)}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/896800/gif.latex)
![ln[cos(t)]sin(t)-\frac{sin^2(t)}{cos(2t)}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/898115/gif.latex)
![ln[sin(t)]cos(t)-\frac{cos^2(t)}{sin(t)}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/898114/gif.latex)







![\frac{dz}{dt}=ln[cos(t)]cos(t)-\frac{sin^2(t)}{cos(t)}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/896804/gif.latex)















 +3[(t^4-10t^3+25t^2)-2(3t^3-15t^2+4t^2-20t)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/898020/gif.latex)
 +3[t^4-10t^3+25t^2-6t^3+30t^2-8t^2+40t]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/898021/gif.latex)
 +3[t^4-16t^3+47t^2+40t]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/898022/gif.latex)

































+[14(1/t)(5t^2-t)](10t-1)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/896834/gif.latex)
+[(14/t)(5t^2-t)](10t-1)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/896835/gif.latex)
+(70t-14)(10t-1)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/896836/gif.latex)















+[sin(x)(-sin(y))](-1)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/896863/gif.latex)