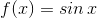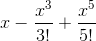Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 2 : Series in Calculus

Study concepts, example questions & explanations for Calculus 2

Create An Account

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : Maclaurin Series

Write out the first three terms for the Maclaurin series of the following function:

$f(x)=10\cos(x)$

Possible Answers:

0+10x+0

10+0-5x^2

0+0+0

10+0+5x^2

Correct answer:

10+0-5x^2

Explanation:

The Maclaurin series for any function is simply the Taylor series of the function about a=0:

$\sum_{n=0}^{\infty }f^{(n)}(a)\frac{(x-a)^n}{n!}$

We first must find the zeroth, first, and second derivative of the function (for n=0, 1, and 2). The zeroth derivative is the function itself:

$f'(x)=-10\sin(x)$

$f''(x)=-10\cos(x)$

The derivatives were found using the following rules:

$\frac{\mathrm{d}}{\mathrm{d} x}\sin(x)=\cos(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x}\cos(x)=-\sin(x)$

Now, we just use the formula, with x=a=0 , to write out the first three terms of the series (n=0, 1, and 2):

$\frac{10(1)(x)^0}{0!}-\frac{10(0)(x)^1}{1!}-\frac{10(1)(x)^2}{2!}=10+0+5x^2$

Report an Error

Example Question #11 : Maclaurin Series

Write the first two terms Maclaurin series of the following function:

$f(x)=x\cos(x)$

Possible Answers:

x+1

0+0

0-x

0+x

Correct answer:

0+x

Explanation:

The Maclaurin series for a function is simply the Taylor series for the function about a=0:

$\sum_{n=0}^{\infty }f^{(n)}(a)\frac{(x-a)^n}{n!}$

We must find the first two terms of the series, corresponding to n=0 and n=1. We need the zeroth and first derivative of the function, the zeroth derivative being the the function itself:

$f'(x)=\cos(x)-x\sin(x)$

The derivative was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$ , $\frac{\mathrm{d} }{\mathrm{d} x} \cos(x)=-\sin(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} f(x)g(x)=f'(x)g(x)+f(x)g'(x)$

Now, use the formula above to write out the first two terms:

$\frac{0(x)^0}{0!}+\frac{1(x)^1}{1!}=0+x$

Report an Error

Example Question #11 : Maclaurin Series

Write out the first five terms of the Maclaurin series for the following function:

$f(x)=\cos(x)$

Possible Answers:

0+0+0+0+0

$0+x+0+\frac{x^3}{6}+0$

$1+0+\frac{x^2}{2}+0+\frac{x^4}{4}$

$1+0-\frac{x^2}{2}+0+\frac{x^4}{24}$

Correct answer:

$1+0-\frac{x^2}{2}+0+\frac{x^4}{24}$

Explanation:

The Maclaurin series for any function is simply the Taylor series for the function about a=0:

$\sum_{n=0}^{\infty }f^{(n)}(a)\frac{(x-a)^n}{n!}$

First, we must find the zeroth through fourth derivative of the function. The zeroth derivative is simply the function itself.

$f'(x)=-\sin(x)$

$f''(x)=-\cos(x)$

$f'''(x)=\sin(x)$

$f^4(x)=\cos(x)$

The following rules were used for the derivatives:

$\frac{d}{dx}\cos(x)=-\sin(x)$ , $\frac{d}{dx}\sin(x)=-\cos(x)$

Next, we simply evaluate all of the derivatives at x=a=0 and then write out all of the terms:

$\frac{1(x)^0}{0!}-\frac{0(x)^1}{1!}-\frac{1(x)^2}{2!}+\frac{0(x)^3}{3!}+\frac{1(x)^4}{4!}$

which simplified is equal to

$1+0-\frac{x^2}{2}+0+\frac{x^4}{24}$

Report an Error

Example Question #314 : Series In Calculus

Write out the first four terms of the Maclaurin series for the following function:

f(x)=2x^2+x+1

Possible Answers:

0+x+2x^2+0

1+x+2x^2+0

0+0+0+0

1+x+4x^2+0

Correct answer:

1+x+2x^2+0

Explanation:

The Maclaurin series is the Taylor series for a function about a=0:

$\sum_{n=0}^{\infty }f^{(n)}(a)\frac{(x-a)^n}{n!}$

We need to find the zeroth, first, second, and third derivative of the function (n=0, 1, 2, and 3). The zeroth derivative is simply the function itself.

f'(x)=4x+1

f''(x)=4

f'''(x)=0

The derivatives were found using the following rule:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

Now, use the above formula, with x=a=0 to write out the first four terms:

$\frac{(1)(x)^0}{0!}+\frac{1(x)^1}{1!}+\frac{4(x)^2}{2!}+\frac{0(x)^3}{3!}$

which simplified becomes

1+x+2x^2+0

Report an Error

Example Question #315 : Series In Calculus

Write the first two terms of the Maclaurin series for the following function:

$f(x)=2x^2-\cos(x)$

Possible Answers:

1+0

-1+0

0+1

0+0

Correct answer:

-1+0

Explanation:

The Maclaurin series for any function is simply the Taylor series for the function about a=0:

$\sum_{n=0}^{\infty }f^{(n)}(a)\frac{(x-a)^n}{n!}$

For the first two terms (n=0, 1) we must find the zeroth and first derivative of the function. The zeroth derivative is just the function itself.

$f'(x)=4x+\sin(x)$

Now, using the above formula, write out the first two terms:

$\frac{-1(x)^0}{0!}+\frac{0(x)^1}{1!}=-1+0$

Report an Error

Example Question #1 : Maclaurin Series For Exponential And Trigonometric Functions

Find the Maclaurin Series of the function

$f(x)=sin\,x$

up to the fifth degree.

Possible Answers:

DNE

$1-\frac{x^2}{2!}+\frac{x^4}{4!}$

$x-\frac{x^3}{3!}+\frac{x^5}{5!}$

$x+\frac{x^2}{2!}-\frac{x^3}{3!}-\frac{x^4}{4!}+\frac{x^5}{5!}$

Correct answer:

$x-\frac{x^3}{3!}+\frac{x^5}{5!}$

Explanation:

The formula for an i-th degree Maclaurin Polynomial is

$f(x)=\sum_{n=0}^{i}\frac{f^{(n)}(0)}{n!}x^n$

For the fifth degree polynomial, we must evaluate the function up to its fifth derivative.

$\begin{matrix} f(0)=sin(0)=0\\ f'(0)=cos(0)=1\\ f''(0)=-sin(0)=0\\ f'''(0)=-cos(0)=-1\\ f^{(4)}=sin(0)=0 \\ \end{matrix}$

$f^{(5)}(0)=cos(0)=1$

The summation becomes

$\sum_{n=0}^{5}\frac{f^{(n)}(0)}{n!}x^n=\frac{f(0)}{0!}x^0+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+\frac{f^{(4)}(0)}{4!}x^4+\frac{f^{(5)}(0)}{5!}x^5$

And substituting for the values of the function and the first five derivative values, we get the Maclaurin Polynomial

$f(x)=sin(x)\approx x-\frac{x^3}{3!}+\frac{x^5}{5!}$

Report an Error

Example Question #316 : Series In Calculus

Given the Maclaurin Series for the following function, write the summation of the series.

y(x)=e^x+sin(x)

Possible Answers:

$\sum_{n=0}^{\infty}x^n$

$\sum_{n=0}^{\infty}x^n\left(\frac{1}{n!}+\frac{(-1)^n*x^{n}}{(1+n)!}\right)$

$\sum_{n=0}^{\infty}x^n\left(\frac{1}{n!}+\frac{(-1)^n*x^{1+n}}{(1+2n)!}\right)$

$\sum_{n=0}^{\infty}x^n\left(\frac{1}{n!}+\frac{(-1)^n}{(1+2n)!}\right)$

Correct answer:

$\sum_{n=0}^{\infty}x^n\left(\frac{1}{n!}+\frac{(-1)^n*x^{1+n}}{(1+2n)!}\right)$

Explanation:

The Maclaurin series for e^x is given by

$e^x= \sum_{n=0}^{\infty }\frac{x^n}{n!}= 1+x+\frac{x^2}{2}+\frac{x^3}{6}+...$

The Maclaurin Series for sin(x) is given by

$sin(x)=\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)!}(x)^{2n+1}=x-\frac{x^3}{6}+\frac{x^5}{120}+...$

Since the question asked

e^x+sin(x)

To write this sum, we can take out x^n as a common factor for both series:

$\sum_{n=0}^{\infty}x^n\left(\frac{1}{n!}+\frac{(-1)^n*x^{1+n}}{(1+2n)!}\right)$

Report an Error

Example Question #1 : Power Series

Find the radius of convergence for the power series $\sum_{k=0}^{\infty} \frac{x^k}{k!}$ .

Possible Answers:

$\sqrt2$

$\infty$

Correct answer:

$\infty$

Explanation:

You might already recognize this as the power series representation for e^x . Since e^x is well defined for all $x \in \mathbb{R}$ , the radius of convergence is $\infty$ .

If we want to find the radius of covergence using convergence tests, we can use the Ratio Test here. We have-

$\lim_{k\to\infty} \left |\frac{a_{k+1}}{a_k} \right | = \lim_{k\to\infty} \left | \frac{x^{k+1}}{(k+1)!} \frac{k!}{x^k} \right | =\lim_{k\to\infty} \left | \frac{x}{k+1}\right | =$

$\lim_{k\to\infty} \frac{\left | x \right |}{k+1} = \left | x \right | \lim_{k\to\infty} \frac{1}{k+1} = \left | x \right | \cdot 0 = 0$

Since this limit equals regardless of the value of , and the Ratio Test indicates absolute convergence of a series when the above limit is less than , $\sum_{k=0}^{\infty} \frac{x^k}{k!}$ converges for all $x \in \mathbb{R}$ . Hence the radius of convergence is $\infty$ .

Report an Error

Example Question #1 : Power Series

One useful way of determining convergence for power series is via Asymptotic Comparison.

Which of the following functions grows fastest?

Possible Answers:

$x^{1,000,000,000,000}$

$9,999,999,999,999,999,999^{x}$

$x^{x}$

Correct answer:

$x^{x}$

Explanation:

The question does not ask which function is the largest at any given point, it asks which grows fastest. For this question we need to look at all of the terms and determine which function has the dominant term. In this case x^x is the dominate term therefore, it will grow the fastest.

Report an Error

Example Question #1 : Power Series

Express cos(x^2) as a power series.

Possible Answers:

$1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^{6}}{6!}+...$

$1-\frac{x^6}{3!}+\frac{x^{10}}{5!}-\frac{x^{14}}{7!}+...$

$1-\frac{x^4}{2!}+\frac{x^8}{4!}-\frac{x^{12}}{6!}+...$

$1-\frac{x^4}{2!}+\frac{x^6}{4!}-\frac{x^8}{6!}+...$

$1-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...$

Correct answer:

$1-\frac{x^4}{2!}+\frac{x^8}{4!}-\frac{x^{12}}{6!}+...$

Explanation:

Write the correct definition of cosine as a power series.

$cos(x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+...$

Replace with the term x^2 .

$cos(x^2)=1-\frac{x^4}{2!}+\frac{x^8}{4!}-\frac{x^{12}}{6!}+...$

The correct answer is:

$1-\frac{x^4}{2!}+\frac{x^8}{4!}-\frac{x^{12}}{6!}+...$

Report an Error

View Calculus 2 Tutors

John
Certified Tutor

The University of Texas at Arlington, Bachelor of Science, Mathematics. Stanford University, Master of Science, Aerospace Eng...

View Calculus 2 Tutors

Bertha
Certified Tutor

California Institute of Technology, Bachelor's (in progress), Chemical Engineering.

View Calculus 2 Tutors

Sundeep
Certified Tutor

Indian Institute of Technology, Engineering in Computer Science, Electrical Engineering. New York University, Masters in Busi...

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Atlanta, Math Tutors in Phoenix, Math Tutors in Washington DC, Statistics Tutors in Houston, GMAT Tutors in Washington DC, MCAT Tutors in Phoenix, Math Tutors in New York City, Math Tutors in Miami, GRE Tutors in Denver, MCAT Tutors in Dallas Fort Worth

Popular Courses & Classes

Spanish Courses & Classes in Los Angeles, MCAT Courses & Classes in Washington DC, ISEE Courses & Classes in Atlanta, GMAT Courses & Classes in Chicago, LSAT Courses & Classes in Houston, GRE Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in San Diego, Spanish Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Philadelphia

Popular Test Prep

ACT Test Prep in Houston, LSAT Test Prep in Seattle, LSAT Test Prep in New York City, GMAT Test Prep in Philadelphia, MCAT Test Prep in Phoenix, GMAT Test Prep in Phoenix, ACT Test Prep in Phoenix, ACT Test Prep in Philadelphia, SAT Test Prep in New York City, GRE Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 2 : Series in Calculus

Study concepts, example questions & explanations for Calculus 2

All Calculus 2 Resources

Example Questions

Example Question #11 : Maclaurin Series

Example Question #11 : Maclaurin Series

Example Question #11 : Maclaurin Series

Example Question #314 : Series In Calculus

Example Question #315 : Series In Calculus

Example Question #1 : Maclaurin Series For Exponential And Trigonometric Functions

Example Question #316 : Series In Calculus

Example Question #1 : Power Series

Example Question #1 : Power Series

Example Question #1 : Power Series

All Calculus 2 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: