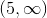All Calculus 1 Resources
Example Questions
Example Question #20 : Increasing Intervals
Find the interval on which the following function is increasing.
never
always
To solve, you must first differentiate the function once and then find where the derivative is positive. To differentiate, use the power rule:
Thus,
Now you must find where this is greater than 0, and therefore increasing.
Therefore, our answer is when x is greater than 2. Thus, 
Example Question #21 : How To Find Increasing Intervals By Graphing Functions
Find the intervals on which the following function is increasing:

We find the region of decreasing of the function by taking the derivative and setting it equal to zero. Then, we plug numbers to the left and right of the roots into the derivative. If it is positive, the function is increasing.

If we plug in more negative values, the derivative function is positive. Therefore, we must be increasing until we get to 

Example Question #22 : How To Find Increasing Intervals By Graphing Functions
Find the increasing intervals of the following function:
The function is never increasing
To determine the intervals on which the function is increasing, we must find the intervals on which the first derivative is positive.
The first derivative of the function is equal to
and was found using the following rule:
Next, we must find the critical values, at which the first derivative is equal to zero:
Now, using the critical value, we make our intervals:
Note that at the bounds of the interval, the first derivative is neither positive nor negative.
To determine whether the derivative is positive or negative on each interval, simply plug any value on each interval into the first derivative function; on the first interval, the first derivative is negative, and on the second interval it is positive. Thus, the function is increasing on
Example Question #23 : How To Find Increasing Intervals By Graphing Functions
Find the intervals on which the following function is increasing:
To find the intervals on which the function is increasing, we must find the intervals on which the first derivative of the function is positive.
The first derivative of the function is
and was found using the following rule:
Next, we must find the critical values, or values at which the first derivative of the function is equal to zero:
Now, using the critical values, we can create the intervals:
Note that at the endpoints of the intervals, the first derivative is neither positive nor negative.
To determine the sign of the first derivative on each interval, simply plug in any value on each interval into the first derivative function and check the sign. On the first interval, the first derivative is positive, on the second it is negative, and on the third it is positive. Thus, the intervals on which the function is increasing are 
Example Question #24 : How To Find Increasing Intervals By Graphing Functions
Tell whether g(x) is increasing or decreasing on the interval [0,3], and how you know.
The function is decreasing on the interval [0,3], because the first derivative is negative.
The function is decreasing on the interval [0,3], because the first derivative is positive.
The function is increasing on the interval [0,3], because the first derivative is positive.
The function is increasing on the interval [0,3], because the first derivative is negative.
The function is increasing on the interval [0,3], because the first derivative is positive.
Tell whether g(x) is increasing or decreasing on the interval [0,3], and how you know.
To tell if a function is increasing or decreasing, we need to see where its derivative is positive and negative. Wherever the derivative is negative, the function will be decreasing, and vice versa.
So, let' find g'(x)
Recall that the derivative of 

So, we get:
Next, plug in the endpoints of our function and see what we get for a sign:
Positive, so we are increasing at 0
So our endpoints both yield a positive derivative. If we tested any point between them, we would also get a positive derivative.
This means that our function is increasing on the interval [0,3], because our first derivative is positive.
Example Question #25 : How To Find Increasing Intervals By Graphing Functions
Is the function g(x) increasing or decreasing on the interval ?
Increasing, because g'(x) is negative on the interval .
Increasing, because g'(x) is positive on the interval .
Decreasing, because g'(x) is positive on the interval .
Decreasing, because g'(x) is negative on the interval .
Increasing, because g'(x) is positive on the interval .
Is the function g(x) increasing or decreasing on the interval ?
To tell if a function is increasing or decreasing, we need to see if its first derivative is positive or negative. let's find g'(x)
Recall that the derivative of a polynomial can be found by taking each term, multiplying by its exponent and then decreasing the exponent by 1.
Next, we need to see if the function is positive or negative over the given interval.
Begin by finding g'(5)
So, g'(5) is positive. Furthermore, any number greater than 5 will also be positive. This means our function is increasing on the given interval
Increasing, because g'(x) is positive on the interval .
Example Question #1 : How To Find Concave Down Intervals By Graphing Functions
Find the interval(s) where the following function is concave down. Graph to double check your answer.
Never
Always
To find when a function is concave, you must first take the 2nd derivative, then set it equal to 0, and then find between which zero values the function is negative.
First, find the 2nd derivative:
Set equal to 0 and solve:
Now test values on all sides of these to find when the function is negative, and therefore decreasing. I will test the values of -3 and 0.
Since the value that is negative is when x=-3, the interval is decreasing on the interval that includes 0. Therefore, our answer is:
Example Question #1612 : Functions
Find the interval(s) where the following function is concave down. Graph to double check your answer.
Always
Never
To find when a function is concave, you must first take the 2nd derivative, then set it equal to 0, and then find between which zero values the function is negative.
First, find the 2nd derivative:
Set equal to 0 and solve:
Now test values on all sides of these to find when the function is negative, and therefore decreasing. I will test the values of 0 and 6.
Since the value that is negative is when x=0, the interval is decreasing on the interval that includes 0. Therefore, our answer is:
Example Question #2 : How To Find Concave Down Intervals By Graphing Functions
Is 

No, 

No, 

Yes, 

Cannot be determined by the information given
Yes, 

Yes, 

To test concavity, we must first find the second derivative of f(x)
This function is concave down anywhere that f''(x)<0, so...
So,

So on the interval -5,-4 f(x) is concave down because f''(x) is negative.
Example Question #1 : Concave Down Intervals
Is 
![[5,7]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/337522/gif.latex)
Concave down, because 

Concave up, because 
Concave up, because 
Concave down, because 
Concave up, because 
To test concavity, we need to perform the second derivative test. Bascially, assuming that our function is twice-differentiable, anywhere that h"(t) is positive will be concave up, and anywhere h"(t) is negative is concave down. Begin as follows:
Next, we need to evaluate h"(t) on the interval [5,7]
So, our h"(t) is positive on the interval, and therefore h(t) is concave up.
All Calculus 1 Resources