Call Now to Set Up Tutoring:

(888) 888-0446

Basic Geometry : Plane Geometry

Study concepts, example questions & explanations for Basic Geometry

Create An Account

All Basic Geometry Resources

9 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #181 : Triangles

In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?

Possible Answers:

399

423

410

403

Correct answer:

403

Explanation:

In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.

First, recall how to find the area of a triangle.

$\text{Area of Triangle}=\frac{\text{base}\times\text{height}}{2}$

In the figure, we are given the triangle’s hypotenuse, which is also the width of the rectangle. We can then use this information and the Pythagorean theorem to find the length of the sides of the triangle.

$\text{Hypotenuse}^2=\text{base}^2+\text{height}^2$

Now, because this is a right isosceles triangle,

$\text{base}=\text{height}$

We can then make the following substitution:

$\text{Hypotenuse}^2=\text{base}^2+\text{base}^2$

$\text{Hypotenuse}^2=2(\text{base})^2$

$\text{Hypotenuse}=\sqrt{2(\text{base})^2}$

$\text{Hypotenuse}=\text{base}\sqrt2$

Therefore:

$\text{base}=\frac{\text{Hypotenuse}}{\sqrt2}$

$\text{base}=\frac{\text{Hypotenuse}\sqrt2}{2}$

Substitute in the value of the hypotenuse to find the length of the base:

$\text{base}=\frac{26\sqrt2}{2}$

$\text{base}=13\sqrt2$

Now, substitute this number in to find the area of the triangle.

$\text{Area of Triangle}=\frac{13\sqrt2 \times 13\sqrt2}{2}$

$\text{Area of Triangle}=\frac{338}{2}$

$\text{Area of Triangle}=169$

Next, recall how to find the area of the rectangle:

$\text{Area of Rectangle}=\text{length}\times\text{width}$

Substitute in the given information from the question to find the area.

$\text{Area of Rectangle}=22\times 26$

$\text{Area of Rectangle}=572$

Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.

$\text{Area of Shaded Region}=\text{Area of Rectangle}-\text{Area of Triangle}$

$\text{Area of Shaded Region}=572-169$

Solve.

$\text{Area of Shaded Region}=403$

Report an Error

Example Question #189 : Triangles

In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?

Possible Answers:

Correct answer:

Explanation:

In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.

First, recall how to find the area of a triangle.

$\text{Area of Triangle}=\frac{\text{base}\times\text{height}}{2}$

$\text{Hypotenuse}^2=\text{base}^2+\text{height}^2$

Now, because this is a right isosceles triangle,

$\text{base}=\text{height}$

We can then make the following substitution:

$\text{Hypotenuse}^2=\text{base}^2+\text{base}^2$

$\text{Hypotenuse}^2=2(\text{base})^2$

$\text{Hypotenuse}=\sqrt{2(\text{base})^2}$

$\text{Hypotenuse}=\text{base}\sqrt2$

Therefore:

$\text{base}=\frac{\text{Hypotenuse}}{\sqrt2}$

$\text{base}=\frac{\text{Hypotenuse}\sqrt2}{2}$

Substitute in the value of the hypotenuse to find the length of the base:

$\text{base}=\frac{20\sqrt2}{2}$

$\text{base}=10\sqrt2$

Now, substitute this number in to find the area of the triangle.

$\text{Area of Triangle}=\frac{16\sqrt2 \times 16\sqrt2}{2}$

$\text{Area of Triangle}=\frac{512}{2}$

$\text{Area of Triangle}=256$

Next, recall how to find the area of the rectangle:

$\text{Area of Rectangle}=\text{length}\times\text{width}$

Substitute in the given information from the question to find the area.

$\text{Area of Rectangle}=12\times 16$

$\text{Area of Rectangle}=192$

Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.

$\text{Area of Shaded Region}=\text{Area of Rectangle}-\text{Area of Triangle}$

$\text{Area of Shaded Region}=256-192$

Solve.

$\text{Area of Shaded Region}=64$

Report an Error

Example Question #21 : How To Find The Length Of The Side Of A 45/45/90 Right Isosceles Triangle

In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?

Possible Answers:

142

144

148

146

Correct answer:

144

Explanation:

In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.

First, recall how to find the area of a triangle.

$\text{Area of Triangle}=\frac{\text{base}\times\text{height}}{2}$

$\text{Hypotenuse}^2=\text{base}^2+\text{height}^2$

Now, because this is a right isosceles triangle,

$\text{base}=\text{height}$

We can then make the following substitution:

$\text{Hypotenuse}^2=\text{base}^2+\text{base}^2$

$\text{Hypotenuse}^2=2(\text{base})^2$

$\text{Hypotenuse}=\sqrt{2(\text{base})^2}$

$\text{Hypotenuse}=\text{base}\sqrt2$

Therefore:

$\text{base}=\frac{\text{Hypotenuse}}{\sqrt2}$

$\text{base}=\frac{\text{Hypotenuse}\sqrt2}{2}$

Substitute in the value of the hypotenuse to find the length of the base:

$\text{base}=\frac{24\sqrt2}{2}$

$\text{base}=12\sqrt2$

Now, substitute this number in to find the area of the triangle.

$\text{Area of Triangle}=\frac{12\sqrt2 \times 12\sqrt2}{2}$

$\text{Area of Triangle}=\frac{288}{2}$

$\text{Area of Triangle}=144$

Next, recall how to find the area of the rectangle:

$\text{Area of Rectangle}=\text{length}\times\text{width}$

Substitute in the given information from the question to find the area.

$\text{Area of Rectangle}=12\times 24$

$\text{Area of Rectangle}=288$

Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.

$\text{Area of Shaded Region}=\text{Area of Rectangle}-\text{Area of Triangle}$

$\text{Area of Shaded Region}=288-144$

Solve.

$\text{Area of Shaded Region}=144$

Report an Error

Example Question #191 : Triangles

In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?

Possible Answers:

195

225

215

205

Correct answer:

195

Explanation:

In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.

First, recall how to find the area of a triangle.

$\text{Area of Triangle}=\frac{\text{base}\times\text{height}}{2}$

$\text{Hypotenuse}^2=\text{base}^2+\text{height}^2$

Now, because this is a right isosceles triangle,

$\text{base}=\text{height}$

We can then make the following substitution:

$\text{Hypotenuse}^2=\text{base}^2+\text{base}^2$

$\text{Hypotenuse}^2=2(\text{base})^2$

$\text{Hypotenuse}=\sqrt{2(\text{base})^2}$

$\text{Hypotenuse}=\text{base}\sqrt2$

Therefore:

$\text{base}=\frac{\text{Hypotenuse}}{\sqrt2}$

$\text{base}=\frac{\text{Hypotenuse}\sqrt2}{2}$

Substitute in the value of the hypotenuse to find the length of the base:

$\text{base}=\frac{26\sqrt2}{2}$

$\text{base}=13\sqrt2$

Now, substitute this number in to find the area of the triangle.

$\text{Area of Triangle}=\frac{13\sqrt2 \times 13\sqrt2}{2}$

$\text{Area of Triangle}=\frac{338}{2}$

$\text{Area of Triangle}=169$

Next, recall how to find the area of the rectangle:

$\text{Area of Rectangle}=\text{length}\times\text{width}$

Substitute in the given information from the question to find the area.

$\text{Area of Rectangle}=14\times 26$

$\text{Area of Rectangle}=364$

Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.

$\text{Area of Shaded Region}=\text{Area of Rectangle}-\text{Area of Triangle}$

$\text{Area of Shaded Region}=364-169$

Solve.

$\text{Area of Shaded Region}=195$

Report an Error

Example Question #192 : 45/45/90 Right Isosceles Triangles

In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?

Possible Answers:

135

145

150

165

Correct answer:

135

Explanation:

In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.

First, recall how to find the area of a triangle.

$\text{Area of Triangle}=\frac{\text{base}\times\text{height}}{2}$

$\text{Hypotenuse}^2=\text{base}^2+\text{height}^2$

Now, because this is a right isosceles triangle,

$\text{base}=\text{height}$

We can then make the following substitution:

$\text{Hypotenuse}^2=\text{base}^2+\text{base}^2$

$\text{Hypotenuse}^2=2(\text{base})^2$

$\text{Hypotenuse}=\sqrt{2(\text{base})^2}$

$\text{Hypotenuse}=\text{base}\sqrt2$

Therefore:

$\text{base}=\frac{\text{Hypotenuse}}{\sqrt2}$

$\text{base}=\frac{\text{Hypotenuse}\sqrt2}{2}$

Substitute in the value of the hypotenuse to find the length of the base:

$\text{base}=\frac{30\sqrt2}{2}$

$\text{base}=15\sqrt2$

Now, substitute this number in to find the area of the triangle.

$\text{Area of Triangle}=\frac{15\sqrt2 \times 15\sqrt2}{2}$

$\text{Area of Triangle}=\frac{450}{2}$

$\text{Area of Triangle}=225$

Next, recall how to find the area of the rectangle:

$\text{Area of Rectangle}=\text{length}\times\text{width}$

Substitute in the given information from the question to find the area.

$\text{Area of Rectangle}=12\times 30$

$\text{Area of Rectangle}=360$

Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.

$\text{Area of Shaded Region}=\text{Area of Rectangle}-\text{Area of Triangle}$

$\text{Area of Shaded Region}=360-225$

Solve.

$\text{Area of Shaded Region}=135$

Report an Error

Example Question #193 : 45/45/90 Right Isosceles Triangles

In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?

Possible Answers:

120

180

150

Correct answer:

120

Explanation:

In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.

First, recall how to find the area of a triangle.

$\text{Area of Triangle}=\frac{\text{base}\times\text{height}}{2}$

$\text{Hypotenuse}^2=\text{base}^2+\text{height}^2$

Now, because this is a right isosceles triangle,

$\text{base}=\text{height}$

We can then make the following substitution:

$\text{Hypotenuse}^2=\text{base}^2+\text{base}^2$

$\text{Hypotenuse}^2=2(\text{base})^2$

$\text{Hypotenuse}=\sqrt{2(\text{base})^2}$

$\text{Hypotenuse}=\text{base}\sqrt2$

Therefore:

$\text{base}=\frac{\text{Hypotenuse}}{\sqrt2}$

$\text{base}=\frac{\text{Hypotenuse}\sqrt2}{2}$

Substitute in the value of the hypotenuse to find the length of the base:

$\text{base}=\frac{24\sqrt2}{2}$

$\text{base}=12\sqrt2$

Now, substitute this number in to find the area of the triangle.

$\text{Area of Triangle}=\frac{12\sqrt2 \times 12\sqrt2}{2}$

$\text{Area of Triangle}=\frac{288}{2}$

$\text{Area of Triangle}=144$

Next, recall how to find the area of the rectangle:

$\text{Area of Rectangle}=\text{length}\times\text{width}$

Substitute in the given information from the question to find the area.

$\text{Area of Rectangle}=11\times 24$

$\text{Area of Rectangle}=264$

Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.

$\text{Area of Shaded Region}=\text{Area of Rectangle}-\text{Area of Triangle}$

$\text{Area of Shaded Region}=264-144$

Solve.

$\text{Area of Shaded Region}=120$

Report an Error

Example Question #191 : 45/45/90 Right Isosceles Triangles

If the length of one leg of a right isosceles triangle is 16cm, what is the length of the other leg?

Possible Answers:

$8\text{ cm}$

$6\text{ cm}$

$32\text{ cm}$

$16\text{ cm}$

$45\text{ cm}$

Correct answer:

$16\text{ cm}$

Explanation:

First we need to know that a right isosceles triangle has two legs with the same length.

In this case we do not need to worry about the hypotenuse.

Since one leg measures 16 cm, the other leg is the same length and so our answer is 16cm.

Report an Error

Example Question #1 : How To Find If Right Triangles Are Similar

$\bigtriangleup ABC \sim \bigtriangleup DEF$ ; $\angle F$ is a right angle; $\overline{AB}=20$ ; $\overline{AC}=10$ ; $\overline{DE}=30$

Find $\overline{EF}$ .

Possible Answers:

$10 \sqrt{3}$

$15 \sqrt{3}$

$30\sqrt{3}$

Correct answer:

$15 \sqrt{3}$

Explanation:

Since $\bigtriangleup ABC \sim \bigtriangleup DEF$ and $\angle F$ is a right angle, $\angle C$ is also a right angle.

$\overline{AB}$ is the hypotenuse of the first triangle; since one of its legs $\overline{AC}$ is half the length of that hypotenuse, $\bigtriangleup ABC$ is 30-60-90 with $\overline{AC}$ the shorter leg and $\overline{BC}$ the longer.

Because the two are similar triangles, $\overline{DE}$ is the hypotenuse of the second triangle, and $\overline{EF}$ is its longer leg.

Therefore, $EF = \frac{\sqrt{3}}{2} \cdot DE = \frac{\sqrt{3}}{2} \cdot 30 = 15 \sqrt{3}$ .

Report an Error

Example Question #1173 : Basic Geometry

Which of the following is sufficient to say that two right triangles are similar?

Possible Answers:

Two of the sides are the same.

All the angles are congruent.

Two sides and one angle are congruent.

Two angles and one side are congruent.

Correct answer:

All the angles are congruent.

Explanation:

If all three angles of a triangle are congruent but the sides are not, then one of the triangles is a scaled up version of the other. When this happens the proportions between the sides still remains unchanged which is the criteria for similarity.

Report an Error

Example Question #2 : How To Find If Right Triangles Are Similar

Which of the following statements is true regarding the two triangles?

Possible Answers:

The triangles are not similar because they are not the same size.

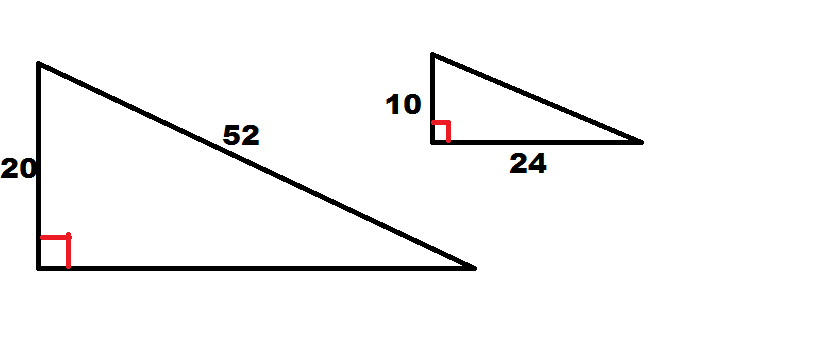
We do not have enough information to show the triangles are similar.

The triangles are similar by Side-Angle-Side

The triangles are similar by Hypotenuse-Leg

The triangles are similar because they are both right triangles.

Correct answer:

The triangles are similar by Side-Angle-Side

Explanation:

Though we must do a little work, we can show these triangles are similar. First, right triangles are not necessarily always similar. They must meet the necessary criteria like any other triangles; furthermore, there is no Hypotenuse-Leg Theorem for similarity, only for congruence; therefore, we can eliminate two answer choices.

However, we can use the Pythagorean Theorem with the smaller triangle to find the missing leg. Doing so gives us a length of 48. Comparing the ratio of the shorter legs in each trangle to the ratio of the longer legs we get

$\frac{20}{10}=\frac{2}{1}$

$\frac{48}{24}=\frac{2}{1}$

In both cases, the leg of the larger triangle is twice as long as the corresponding leg in the smaller triangle. Given that the angle between the two legs is a right angle in each triangle, these angles are congruent. We now have enough evidence to conclude similarity by Side-Angle-Side.

Report an Error

View Tutors

Christine
Certified Tutor

State University of New York at Stony Brook, Bachelor, Political Science.

View Tutors

Lenore Noni
Certified Tutor

Columbia University in the City of New York, Master of Arts, Education.

View Tutors

Thomas
Certified Tutor

California State University-Dominguez Hills, Bachelor in Arts, Studio Arts. University of California-San Diego, Doctor of Phi...

All Basic Geometry Resources

9 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Houston, LSAT Tutors in Chicago, MCAT Tutors in Washington DC, Biology Tutors in Houston, French Tutors in Washington DC, SAT Tutors in Chicago, Computer Science Tutors in Atlanta, English Tutors in Atlanta, Spanish Tutors in Philadelphia, SSAT Tutors in Chicago

Popular Courses & Classes

SAT Courses & Classes in Los Angeles, GRE Courses & Classes in Chicago, ACT Courses & Classes in Philadelphia, ISEE Courses & Classes in Miami, GMAT Courses & Classes in Philadelphia, Spanish Courses & Classes in Phoenix, GMAT Courses & Classes in Washington DC, MCAT Courses & Classes in New York City, GRE Courses & Classes in Los Angeles, SAT Courses & Classes in Washington DC

Popular Test Prep

ACT Test Prep in Philadelphia, SSAT Test Prep in Los Angeles, ISEE Test Prep in Atlanta, GMAT Test Prep in Philadelphia, SSAT Test Prep in Atlanta, GMAT Test Prep in Chicago, SSAT Test Prep in Seattle, GRE Test Prep in Los Angeles, MCAT Test Prep in San Diego, ISEE Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Basic Geometry : Plane Geometry

Study concepts, example questions & explanations for Basic Geometry

All Basic Geometry Resources

Example Questions

Example Question #181 : Triangles

Example Question #189 : Triangles

Example Question #21 : How To Find The Length Of The Side Of A 45/45/90 Right Isosceles Triangle

Example Question #191 : Triangles

Example Question #192 : 45/45/90 Right Isosceles Triangles

Example Question #193 : 45/45/90 Right Isosceles Triangles

Example Question #191 : 45/45/90 Right Isosceles Triangles

Example Question #1 : How To Find If Right Triangles Are Similar

Example Question #1173 : Basic Geometry

Example Question #2 : How To Find If Right Triangles Are Similar

All Basic Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: