All Basic Geometry Resources
Example Questions
Example Question #37 : How To Find The Perimeter Of A 45/45/90 Right Isosceles Triangle
A right isosceles triangle is stacked on top of a square as shown in the figure. Find the perimeter of the compound shape.


Notice that the hypotenuse of the right isosceles triangle is also the length of a side of the square.
First, we will need to find the length of the legs of the triangle by using the Pythagorean theorem.
Substitute in the given length of the hypotenuse to find the length of the leg of the triangle.
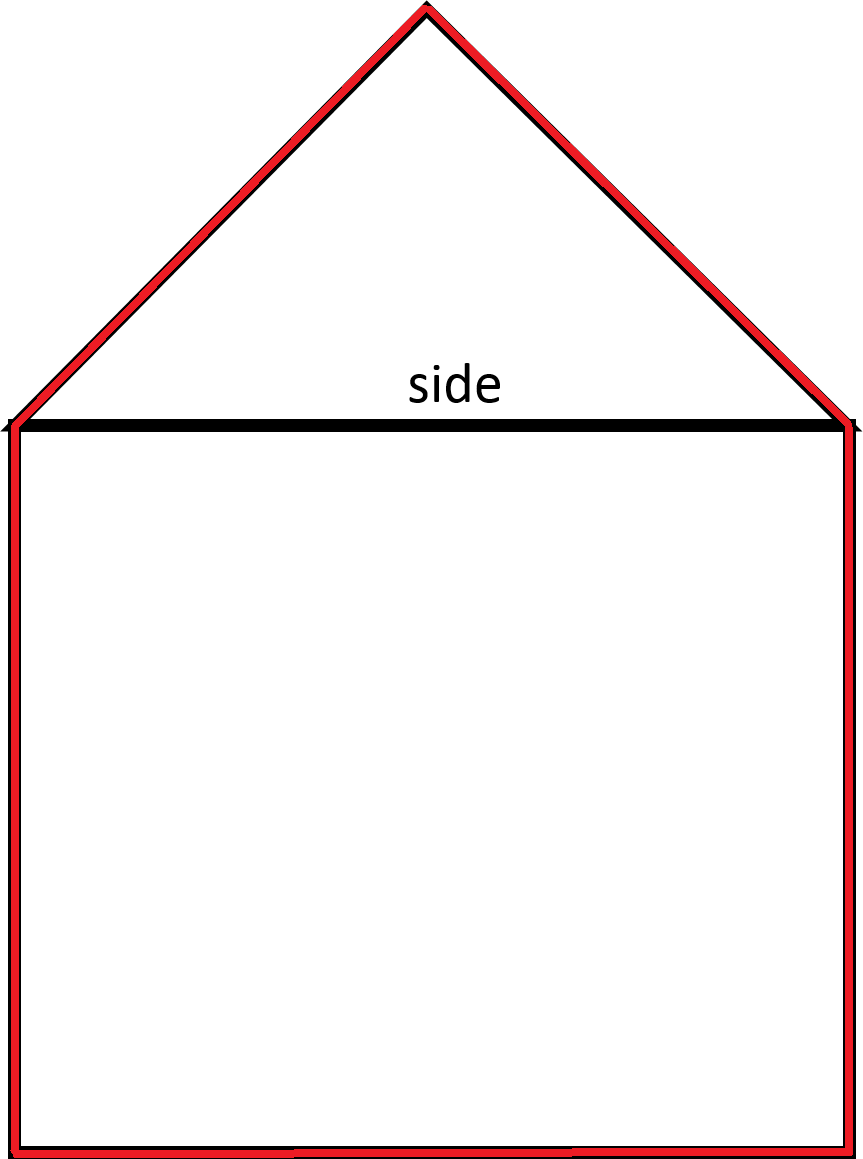
In order to find the perimeter, add up the lengths outlined in red. The perimeter includes the two legs of the triangle and three sides of the square.
Therefore:
Example Question #38 : How To Find The Perimeter Of A 45/45/90 Right Isosceles Triangle
A right isosceles triangle is stacked on top of a square as shown in the figure. Find the perimeter of the compound shape.


Notice that the hypotenuse of the right isosceles triangle is also the length of a side of the square.
First, we will need to find the length of the legs of the triangle by using the Pythagorean theorem.
Substitute in the given length of the hypotenuse to find the length of the leg of the triangle.

In order to find the perimeter, add up the lengths outlined in red. The perimeter includes the two legs of the triangle and three sides of the square.
Therefore:
Example Question #39 : How To Find The Perimeter Of A 45/45/90 Right Isosceles Triangle
A right isosceles triangle is stacked on top of a square as shown in the figure. Find the perimeter of the compound shape.


Notice that the hypotenuse of the right isosceles triangle is also the length of a side of the square.
First, we will need to find the length of the legs of the triangle by using the Pythagorean theorem.
Substitute in the given length of the hypotenuse to find the length of the leg of the triangle.

In order to find the perimeter, add up the lengths outlined in red. The perimeter includes the two legs of the triangle and three sides of the square.
Therefore:
Example Question #1141 : Basic Geometry
A right isosceles triangle is stacked on top of a square as shown in the figure. Find the perimeter of the compound shape.


Notice that the hypotenuse of the right isosceles triangle is also the length of a side of the square.
First, we will need to find the length of the legs of the triangle by using the Pythagorean theorem.
Substitute in the given length of the hypotenuse to find the length of the leg of the triangle.

In order to find the perimeter, add up the lengths outlined in red. The perimeter includes the two legs of the triangle and three sides of the square.
Therefore:
Example Question #41 : How To Find The Perimeter Of A 45/45/90 Right Isosceles Triangle
A right isosceles triangle is stacked on top of a square as shown in the figure. Find the perimeter of the compound shape.


Notice that the hypotenuse of the right isosceles triangle is also the length of a side of the square.
First, we will need to find the length of the legs of the triangle by using the Pythagorean theorem.
Substitute in the given length of the hypotenuse to find the length of the leg of the triangle.

In order to find the perimeter, add up the lengths outlined in red. The perimeter includes the two legs of the triangle and three sides of the square.
Therefore:
Example Question #42 : How To Find The Perimeter Of A 45/45/90 Right Isosceles Triangle
A right isosceles triangle is stacked on top of a square as shown in the figure. Find the perimeter of the compound shape.


Notice that the hypotenuse of the right isosceles triangle is also the length of a side of the square.
First, we will need to find the length of the legs of the triangle by using the Pythagorean theorem.
Substitute in the given length of the hypotenuse to find the length of the leg of the triangle.

In order to find the perimeter, add up the lengths outlined in red. The perimeter includes the two legs of the triangle and three sides of the square.
Therefore:
Example Question #1 : How To Find The Length Of The Side Of A 45/45/90 Right Isosceles Triangle
The perimeter of a 45-45-90 triangle is 100 inches. To the nearest tenth of an inch, what is the length of each leg?
Let 

Therefore,
Example Question #1 : How To Find The Length Of The Side Of A 45/45/90 Right Isosceles Triangle

Example Question #161 : 45/45/90 Right Isosceles Triangles

Example Question #1141 : Plane Geometry
Angle 


Since we know two of the three angles in this triangle, we can calculate the third, 
Therefore this is a 45/45/90 right triangle. Remember that 45/45/90 right triangles are have a leg:leg:hypotenuse ratio of 1:1:
We know the hypotenuse, 


To make this look like one of the answer choies, rationalize the denominator by muliplying the fraction by 
All Basic Geometry Resources








































































































