The Similar Figures Theorem holds that similar figures have both equal corresponding angles and proportional corresponding lengths. Either condition alone is not sufficient.  If two figures have both equal corresponding angles and equal corresponding lengths then they are congruent, not similar.

The Similar Figures Theorem holds that similar figures have both equal corresponding angles and proportional corresponding lengths. In other words, we need to know both the measures of the corresponding angles and the lengths of the corresponding sides. In this case, we know only the measures of  and . We don't know the measures of any of the other angles or the lengths of any of the sides, so we cannot answer the question -- they might be similar, or they might not be.

It's not enough to know that both figures are right triangles, nor can we assume that angles are the same measurement because they appear to be.

Similar triangles do not have to be the same size.

Since  and  are similar triangles, we know that they have proportional corresponding lengths.  We must determine which sides correspond.  Here, we know  corresponds to  because both line segments lie opposite  angles and between  and  angles. Likewise, we know corresponds to  because both line segments lie opposite  angles and between  and  angles.  We can use this information to set up a proportion and solve for the length of .

Substitute the known values.

Cross-multiply and simplify.

 and  result from setting up an incorrect proportion.  results from incorrectly multiplying  and .

These triangles were purposely drawn misleadingly. Just from glancing at them, the angles that appear to correspond are given different angle measures, so they don't "look" similar. However, if we subtract, we figure out that the missing angle in the triangle with the 66-degree angle must be 24 degrees, since . Similarly, the missing angle in the triangle with the 24-degree angle must be 66 degress. This means that all 3 corresponding pairs of angles are congruent, making the triangles similar.

The two triangles are similar, but we can't be sure of that until we can compare all three corresponding pairs of sides and make sure the ratios are the same. In order to do that, we first have to solve for the missing sides using the Pythagorean Theorem.

The smaller triangle is missing not the hypotenuse, c, but one of the legs, so we'll use the formula slightly differently.

subtract 36 from both sides

Now we can compare all three ratios of corresponding sides:

one way of comparing these ratios is to simplify them.

We can simplify the leftmost ratio by dividing top and bottom by 3 and getting  . 

We can simplify the middle ratio by dividing top and bottom by 4 and getting .

Finally, we can simplify the ratio on the right by dividing top and bottom by 5 and getting .

This means that the triangles are definitely similar, and is the scale factor.

In order to compare these triangles and determine if they are similar, we need to know all three side lengths in both triangles. To get the missing ones, we can use Pythagorean Theorem:

take the square root

The other triangle is missing one of the legs rather than the hypotenuse, so we'll adjust accordingly:

subtract 36 from both sides

Now we can compare ratios of corresponding sides:

The first ratio simplifies to , but we can't simplify the others any more than they already are. The three ratios clearly do not match, so these are not similar triangles.

If we seek to prove that , then , , and  correspond to , , and , respectively.

By the Side-Angle-Side Similarity Theorem (SASS), if two sides of a triangle are in proportion with the corresponding sides of another triangle, and the included angles are congruent, then the triangles are similar. 

 and , so by the Division Property of Equality, . Also,  and , their respective included angles, are both right angles, so . The conditions of SASS are met, so 

The distance from the origin to  is the absolute value of the -coordinate of , which is . Similarly, , , and . Also, since the axes intersect at right angles,  and  are both right, and, consequently, congruent. 

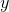
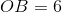
According to the Side-Angle-Side Similarity Theorem (SASS), if two sides of a triangle are in proportion to the corresponding sides of a second triangle, and their included angles are congruent, the triangles are similar. 

We can test the proportion statement 

by substituting:

Test the truth of this statement by comparing their cross products:

The cross-products are equal, making the proportion statement true, so two pairs of sides are in proportion. Also, their included angles   and  are congruent. This sets up the conditions of SASS, so .

 is an altitude of , so it divides the triangle into two smaller triangles similar to each other - that is, if we match the shorter legs, the longer legs, and the hypotenuses, the similarity statement is

.

Rearrange the Pythagorean Theorem to find the missing side. The Pythagorean Theorem is:

 where  is the hypotenuse and and  are the sides.