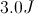The force of friction is what keeps the car in circular motion, preventing it from flying off the track. In other words, the frictional force will be equal to the centripetal force.

We can cancel mass from either side of the equation and rearrange to solve for the coefficient of friction:

We can use our given values to solve:

The time for one full revolution can be calculated simply by manipulating the defintion of velocity, where the distance is just the circumference of the circlular path. The time it takes is modeled by the following equation: 



Use the given radius and velocity to solve for the time per revolution:

The law of conservation of energy states:

If the car starts at rest, then the initial kinetic energy = 0 J.

If the car ends at the reference height, the final potential energy = 0 J. 

Subsituting these values, the equation becomes:

The initial potential energy can be determined by:

The final kinetic energy equation is:

Substituting the initial potential energy and final kinetic energy into our modified conservation of energy equation, we get:

Kinetic energy is defined by the equation:

Taking the derivative of the position function allows us to obtain the velocity function:

We can now determine the velocity after two seconds:

Now that we know our velocity, we can solve for the kinetic energy.

Kinetic energy is given by the equation:

We can find the velocity using the given acceleration and time:

Use this velocity to find the kinetic energy after three seconds:

The formula for kinetic energy of an object is:

The problem gives us the mass and the kinetic energy, and asks for the velocity, so we can rearrange the equation:

Use our given values for kinetic energy and mass to solve:

First, find out how much the spring compresses when the 4kg box is put on top of it. To find this, consider what forces are acting on the box when it is resting on the spring. The forces acting on it are the upward spring force, , and the downward gravitational force,; thus, the net force acting on the box is given by the equation below.

We have chosen the upward direction to be positive and the downward direction to be negative. The net force is equal to zero because the box is at rest. Solve for x.

Then use this value to find the potential energy of the spring.

So when the box is placed on top of the spring, the spring gains a potential energy of 6.5J.

The equation for potential energy is:

We can rearrange to solve for the height:

Plug in our given values to solve:

We can use conservation of energy to find the velocity required to launch the ball.

In order to launch the ball at a velocity that escapes Earth's gravity, the kinetic energy must overcome the gravitational pull of the Earth. We can use conservation of energy to make the kinetic energy and gravitational potential energies equivalent.

Rearrange to solve for the escape velocity:

Finally, plug in our values and solve.