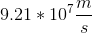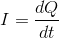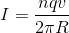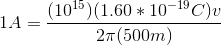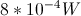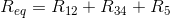Call Now to Set Up Tutoring:

(888) 888-0446

AP Physics C Electricity : AP Physics C

Study concepts, example questions & explanations for AP Physics C Electricity

Create An Account

All AP Physics C Electricity Resources

1 Diagnostic Test 46 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Current

A particle accelerator with a radius of 500 meters can have up to $10^{15}$ protons circulating within it at once.

$q_{proton}=1.60*10^{-19}C$

How fast must the protons in the accelerator move in order to produce a current of 1A?

Possible Answers:

$3.00*10^8\frac{m}{s}$

$2.04*10^8\frac{m}{s}$

$9.21*10^{7}\frac{m}{s}$

$1.96*10^7\frac{m}{s}$

$1.95*10^6\frac{m}{s}$

Correct answer:

$1.96*10^7\frac{m}{s}$

Explanation:

The current produced is the total charge that circulates the particle accelerator per unit time.

$I=\frac{dQ}{dt}$

We calculate this by the equation:

$I = \frac{nqv}{2\pi R}$

is the number of protons, is the charge per proton, is the velocity of each proton, and is the radius of the particle accelerator.

Using the given current, we then solve for the velocity:

$1A = \frac{(10^{15})(1.60*10^{-19}C)v}{2\pi (500m)}$

$v=\frac{(1A)2\pi(500m)}{(10^{15})(1.60*10^{-19}C)}= 1.96*10^7\frac{m}{s}$

Report an Error

Example Question #1 : Interpreting Circuit Diagrams

Three resistors R₁, R₂, and R₃ and the capacitor, C, are connected to an ideal battery V to complete the circuit as shown.

Ps0_capacitorcircuit

After the circuit has been connected for a very long time, the currents in each branch of the circuit are measured to be some values I_1 , , and , and the charge on the capacitor some value .

Which of the following equations is a correct expression regarding the voltage of the circuit after a long time?

Possible Answers:

$0=-\frac{Q}{}C-R_{3}I_{3} -R_{2}I_{2}$

$0=+V-\frac{Q}{}C-R_{3}I_{3} -R_{1}I_{1}$

$0=+V-\frac{Q}{}C-R_{3}I_{3} -R_{2}I_{2}$

$0=-V-R_{2}I_{2} -R_{1}I_{1}$

Correct answer:

$0=+V-\frac{Q}{}C-R_{3}I_{3} -R_{1}I_{1}$

Explanation:

Identifying the sum of the voltage drops and rises (Kirchoff's Loop Law) around the three possible loops of this circuit is the key to answering this question correctly. The following signs can be assigned to each of the circuit elements based on the direction of the currents given.

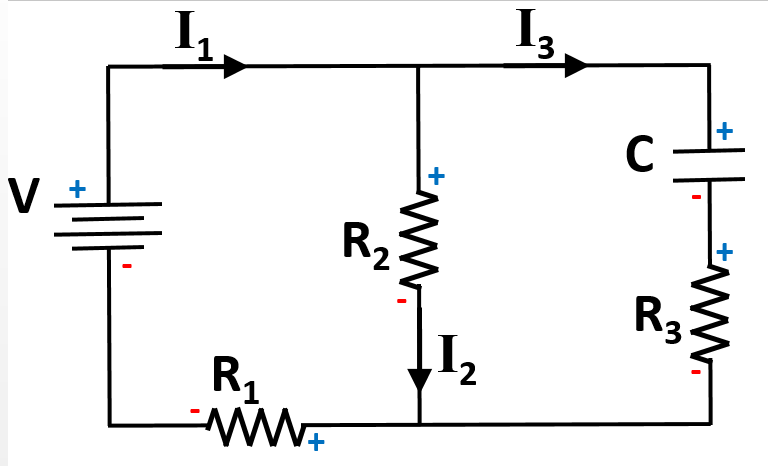
Ps0_capacitorcircuit_2

Use Ohm's law and the equation for capacitance to derive terms for the voltage across each element of the circuit.

V=IR

$C=\frac{Q}{V}\rightarrow V=\frac{Q}{C}$

There are three possible paths through the circuit, resulting in three correct equations that could be derived:

$0=+V-\frac{Q}{}C-R_{3}I_{3} -R_{1}I_{1}$

$0=-\frac{Q}{}C-R_{3}I_{3} +R_{2}I_{2}$

$0=+V-R_{2}I_{2} -R_{1}I_{1}$

Only one of the given answer options matches up correctly to these.

Report an Error

Example Question #1 : Using Ohm's Law

A simple circuit consists of a $2\ \text{M}\Omega$ resistor that's connected to a battery. How much power is dissipated by the resistor?

Possible Answers:

$5.5*10^{-6}W$

$4*10^{-5}W$

$2*10^{-2}W$

$7.2*10^{-2}W$

$8*10^{-4}W$

Correct answer:

$4*10^{-5}W$

Explanation:

One of the formulas for power is $P=\frac{V^2}{R}$ . We are given the values of the voltage and resistance.

$V=9\ \text{V}$

$R=2\ \text{M}\Omega=2*10^6\ \Omega$

Using these values, we can solve for power.

$P=\frac{(9\ \text{V})^2}{2*10^6\ \Omega}$

$P=4*10^{-5}\ \text{W}$

Report an Error

Example Question #71 : Electricity And Magnetism Exam

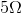
A cicuit with a voltage source of 40V has a $15\Omega$ resistor and a $5\Omega$ resistor in series, followed by two $5\Omega$ resistors in parallel. After the parallel branches rejoin, there is a $10\Omega$ resistor before the circuit is closed at the voltage source.

What is the current supplied by the source?

Possible Answers:

1.5A

0.82A

1.2A

1.0A

Correct answer:

1.2A

Explanation:

The current supplied by the source can be calculated using a derivation of Ohm's law:

$I=\frac{V}{R}$

Start by finding the equivalent resistance of the circuit.

Sum the first two resistors in series:

$R_{12}=15\Omega+5\Omega=20\Omega$

Calculate the equivalent resistance of the two resistors in parallel:

$\frac{1}{R_{34}}=\frac{1}{5\Omega}+\frac{1}{5\Omega}=\frac{2}{5\Omega}$

$R_{34}=\frac{5}{2}\Omega=2.5\Omega$

Now, all of the reistances can be viewed as being in series.

$R_{eq}=R_{12}+R_{34}+R_{5}$

$R_{eq}=20\Omega+2.5\Omega+10\Omega=32.5\Omega$

Returning to our current calulation, we can find our final answer:

$I=\frac{V}{R}=\frac{40V}{32.5\Omega}=1.2A$

Report an Error

Example Question #1 : Using Ohm's Law

Ps0_resistorcircuit

$R_1=15\Omega,\ R_2=20\Omega,\ R_3=20\Omega$

V=50V

What is the current delivered to the curcuit by the battery?

Possible Answers:

4.6A

1.1A

0.91A

2.0A

Correct answer:

2.0A

Explanation:

Using Ohm's law to solve for the value of the current from the battery requires calculation of the equivalent resistance of the circuit.

$V=IR_{eq}$

The resistors R₂ and R₃ are in parallel with one another. Once combined, their requivalent resistor (R₂₃) is in series with R₁.

Ps0_resistorcircuit_2

The equivalent resistance is thus given by:

$R_{eq}=\left ( \frac{1}{R_{2}} + \frac{1}{R_{3}} \right )^{-1} + R_{1}$

$R_{eq}=\left ( \frac{1}{20\Omega} + \frac{1}{20\Omega} \right )^{-1} + 15\Omega$

$R_{eq}=10\Omega + 15\Omega=25\Omega$

Use this value and the given voltage to solve for the current in the circuit:

$I = \frac{V}{R_{eq}}$

$I=\frac{50V}{25\Omega}=2.0A$

Report an Error

Example Question #1 : Calculating Circuit Power

A straight copper wire has a fixed voltage applied across its length. Which of the following changes would increase the power dissipated by this wire?

Possible Answers:

Increasing the temperature of the wire

Decreasing the cross-sectional area of the wire

Changing the material of the wire to a metal of greater resistivity

None of these options result in increased power dissipation

Decreasing the length of the wire

Correct answer:

Decreasing the length of the wire

Explanation:

Relevant equations:

V = IR

P = IV = I^2 R

$R = \frac{\rho L}{A}$

Current and resistance are inversely proportional to one another, assuming voltage is fixed. Since P = I^2 R , changes in current effect the power more than changes in resistance do. Thus, we need current to increase, meaning that resistance must decrease.

To decrease resistance, we could:

1. Change the material of the wire to one of lesser resistivity

2. Decrease the length of the wire

3. Increase the cross-sectional area of the wire

4. Decrease the temperature of the wire (very slight effect on resistance)

Report an Error

Example Question #72 : Electricity And Magnetism Exam

A simple circuit contains two $12\Omega$ resistors in parallel, connected to a 20V source. What power is being provided by the source to the circuit?

Possible Answers:

42W

56W

67W

20W

Correct answer:

67W

Explanation:

The power supplied to the circuit can be calculated using the equation:

$P=IV=\frac{V^2}{R}$

To use this equation, we need to find the equivalent resistance of the circuit. Use the equation for equivalent resistance in parallel:

$\frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}$

$\frac{1}{R_{eq}}=\frac{1}{12\Omega}+\frac{1}{12\Omega}=\frac{1}{6\Omega}$

$R_{eq}=6\Omega$

Now that we have the resistance and the voltage, we can solve for the power.

$P=\frac{V^2}{R}=\frac{(20V)^2}{6\Omega}\approx 67W$

Report an Error

Example Question #2 : Calculating Circuit Power

A battery is measured to have a potential of 5V. When connected to a wire with no resistors or other components, the voltage measured is 4.9V.

If the current through the wire is measured to be 2A, how much thermal energy is being lost per second as soon as the wire is connected to the battery?

Possible Answers:

0.4W

1.0W

0.2W

0.8W

Correct answer:

0.2W

Explanation:

First, we must know that the wire has some internal resistance . To calculate this, we need to know the potential drop through the wire, which must be the difference we saw from the initial voltage reading to the second. This value, 0.1V, we plug into Ohm's law to calculate the resistance of the wire.

V=IR

0.1V=(2A)R

$R=0.05\Omega$

The question asks for energy lost per second; this value is equivalent to the power.

P=I^2R

Use our values to solve.

$P=(2A)^2(0.05\Omega)=0.2W$

Report an Error

Example Question #1 : Circular Motion

A 1.6kg ball is attached to a 1.8m string and is swinging in circular motion horizontally at the string's full length. If the string can withstand a tension force of 87N, what is the maximum speed the ball can travel without the string breaking?

Possible Answers:

$14.3\frac{m}{s}$

$9.9\frac{m}{s}$

$8.2\frac{m}{s}$

$4.5\frac{m}{s}$

$11.3\frac{m}{s}$

Correct answer:

$9.9\frac{m}{s}$

Explanation:

The ball is experiencing centripetal force so that it can travel in a circular path. This centripetal force is written as the equation below.

$F_c=ma=\frac{mv^2}{r}$

Remember that centripetal acceleration is given by the following equation.

$a=\frac{v^2}{r}$

Since the centripetal force is coming from the tension of the string, set the tension force equal to the centripetal force.

$T=\frac{mv^2}{r}$

Since we're trying to find the speed of the ball, we solve for v.

$v=\sqrt{\frac{Tr}{m}}$

We know the following information from the question.

T=87N

r=1.8m

m=1.6kg

We can use this information in our equation to solve for the speed of the ball.

$v=\sqrt{\frac{(87N)(1.8m)}{1.6kg}}}$

$v=9.9\frac{m}{s}$

Report an Error

Example Question #1 : Circular Motion

In uniform circular motion, the net force is always directed ___________.

Possible Answers:

away from the center of the circle

in the same direction as the tangential velocity

toward the center of the circle

nowhere; the net force will be zero

Correct answer:

toward the center of the circle

Explanation:

The correct answer is "toward the center of the circle." Newton's second law tells us that the direction of the net force will be the same as the direction of the acceleration of the object.

F=ma

In uniform circular motion, the object accelerates towards the center of the circle (centripetal acceleration); the net force acts in the same direction.

Report an Error

View Tutors

Muhammad
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Mechanical Engineering.

View Tutors

Mark
Certified Tutor

Murray State University, Bachelor of Science, Mathematics.

View Tutors

Dossevi
Certified Tutor

cole Ste Genevive Versailles, Bachelor of Science, Mathematics. Institut National Polytechnique de Grenoble, Master of Scienc...

All AP Physics C Electricity Resources

1 Diagnostic Test 46 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Dallas Fort Worth, French Tutors in New York City, ACT Tutors in Boston, LSAT Tutors in New York City, Biology Tutors in Dallas Fort Worth, Reading Tutors in Atlanta, Biology Tutors in Houston, Calculus Tutors in Phoenix, ISEE Tutors in Boston, French Tutors in San Francisco-Bay Area

Popular Courses & Classes

GMAT Courses & Classes in Houston, GRE Courses & Classes in Washington DC, GMAT Courses & Classes in Seattle, MCAT Courses & Classes in Atlanta, LSAT Courses & Classes in Washington DC, GRE Courses & Classes in New York City, ISEE Courses & Classes in Boston, GMAT Courses & Classes in San Diego, GMAT Courses & Classes in Boston, GMAT Courses & Classes in Denver

Popular Test Prep

MCAT Test Prep in Denver, GMAT Test Prep in Houston, GRE Test Prep in San Diego, ISEE Test Prep in Los Angeles, SAT Test Prep in Denver, GMAT Test Prep in Denver, SSAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Seattle, SSAT Test Prep in San Diego, LSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Physics C Electricity : AP Physics C

Study concepts, example questions & explanations for AP Physics C Electricity

All AP Physics C Electricity Resources

Example Questions

Example Question #2 : Current

Example Question #1 : Interpreting Circuit Diagrams

Example Question #1 : Using Ohm's Law

Example Question #71 : Electricity And Magnetism Exam

Example Question #1 : Using Ohm's Law

Example Question #1 : Calculating Circuit Power

Example Question #72 : Electricity And Magnetism Exam

Example Question #2 : Calculating Circuit Power

Example Question #1 : Circular Motion

Example Question #1 : Circular Motion

All AP Physics C Electricity Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: