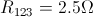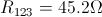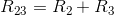Call Now to Set Up Tutoring:

(888) 888-0446

AP Physics C Electricity : AP Physics C

Study concepts, example questions & explanations for AP Physics C Electricity

Create An Account

All AP Physics C Electricity Resources

1 Diagnostic Test 46 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Electric Circuits

The plates of a parallel plate capacitor are 3mm apart and 5m^2 in area. A potential difference of 1000V is applied across the capacitor. Find the capacitance.

$\epsilon_0=8.85*10^{-12} \frac{F}{m}$

Possible Answers:

$1.5*10^{-9}F$

$1.5*10^{-10}F$

$1.5*10^{-8}F$

$1.5*10^{-7}F$

Correct answer:

$1.5*10^{-8}F$

Explanation:

Capacitance is related to plate area and distance by the equation $C=\epsilon_0\frac{A}{d}$ .

Given the area and distance, we can solve for capacitance. The voltage, in this case, is irrelevant.

$C=8.85* 10^{-12} \frac{F}{m}(\frac{5 m^2}{3*10^{-3}m})=8.85* 10^{-12} \frac{F}{m}(1.67*10^{3}m)=1.5*10^{-8}F$

Report an Error

Example Question #2 : Electric Circuits

The plates of a parallel plate capacitor are 3mm apart and 5m^2 in area. A potential difference of 1000V is applied across the capacitor. Compute the charge on each plate.

$\epsilon_0=8.85* 10^{-12} \frac{F}{m}$

Possible Answers:

$1.5*10^{-8}C$

$1.5*10^{-7}C$

$1.5*10^{-5}C$

$1.5*10^{-6}C$

Correct answer:

$1.5*10^{-5}C$

Explanation:

Charge on a capacitor is given by the equation Q=CV . We know that the voltage is 1000V , but we need to determine the capacitance based off of the area and distance between the plates.

$C=\epsilon_0\frac{A}{d}$

$C=(8.85*10^{-12}\frac{F}{m})(\frac{5m^2}{3*10^{-3}m})$

$C=(8.85*10^{-12}\frac{F}{m})(1.67*10^{3}m)=1.5*10^{-8}F$

We can plug this value into the equation for charge.

$Q=CV=(1.5*10^{-8}F)(1000V)$

$Q=1.5*10^{-5}C$

Report an Error

Example Question #3 : Capacitors

The plates of a parallel plate capacitor are 3mm apart. A potential difference of 1000V is applied across the capacitor. Compute the magnitude of the generated electric field.

$\epsilon_0=8.85*10^{-12}\frac{F}{m}$

Possible Answers:

$3.33*10^4\frac{N}{C}$

$3.33*10^5\frac{N}{C}$

$3.33*10^6\frac{N}{C}$

$3.33*10^3\frac{N}{C}$

Correct answer:

$3.33*10^5\frac{N}{C}$

Explanation:

The electric field given by a capacitor is given by the formula $E=\frac{Q}{\epsilon_0 A}$ . We do not have these variables, so we will have to adjust the equation.

$Q=CV\rightarrow E=\frac{CV}{\epsilon_0A}$

The capacitance can be determined by the area of the plates and the distance between them.

$C=\epsilon_0\frac{A}{d}\rightarrow E=\frac{\epsilon_0\frac{A}{d}V}{\epsilon_0A}$

This equation simplifies to $E=\frac{V}{d}$ , allowing us to solve using the values given in the question.

$E=\frac{1000V}{3*10^{-3}m}=3.33*10^{5}\frac{N}{C}$

Report an Error

Example Question #4 : Capacitors

If two identical parallel plate capacitors of capacitance are connected in series, which is true of the equivalent capacitance, $C_{eq}$ ?

Possible Answers:

$C_{eq}= 2C$

$C_{eq}=\frac{C}{2}$

$\frac{C}{2} < C_{eq} < C$

$C < C_{eq}< 2C$

$C_{eq}=C$

Correct answer:

$C_{eq}=\frac{C}{2}$

Explanation:

Relevant equations:

$\frac{1}{C_{eq, series}}=\frac{1}{C_1}+\frac{1}{C_2}+ ...$

Use the series equation, replacing C1 and C2 with the given constant C:

$\frac{1}{C_{eq, series}}= \frac{1}{C}+ \frac{1}{C}$

$\frac{1}{C_{eq, series}}=\frac{2}{C}$

$C_{eq, series} = \frac{C}{2}$

This agrees with the general rule that the equivalent capacitance in series is less than the capacitance of any of the individual capacitors.

Report an Error

Example Question #4 : Capacitors

Two parallel conducting plates each have an area of and are separated by a distance, . One plate has a charge evenly distributed across it, and the other has a charge of . A proton (charge ) is initially held near the positive plate, then released such that it accelerates towards the negative plate. How much kinetic energy has the proton gained in this process?

Possible Answers:

$\frac{eQ \epsilon _o A}{d^2}$

$\frac{eQ}{\epsilon _o A d}$

$\frac{eQd}{\epsilon _oA}$

$\frac{e \epsilon _o A}{Qd}$

$\frac{eQ\epsilon _o A}{d}$

Correct answer:

$\frac{eQd}{\epsilon _oA}$

Explanation:

Relevant equations:

$W = q\Delta V$

$W = \Delta KE$

$C = \frac{Q}{V}$

$C = \frac{\epsilon _o A}{d}$

According to the work-energy theorem, work done on the proton is equal to its change in kinetic energy.

1. Find an expression for potential difference, , in terms of and , by setting the two capacitance equations equal to each other:

$\frac{Q}{V}=\frac{\epsilon _o A}{d}$

$V = \frac{Qd}{\epsilon _o A}$

2. Multiply the potential difference times the proton charge to find work (and thus kinetic energy):

$W = \frac {eQd}{\epsilon _o A} = \Delta K$

Report an Error

Example Question #3 : Electric Circuits

A $5 \mu F$ and $10 \mu F$ capacitor are connected in series with a 12V battery. What is the magnitude of the charge on one plate of the $5 \mu F$ capacitor?

Possible Answers:

$40 \mu C$

$180 \mu C$

$2.4 \mu C$

$10 \mu C$

$60 \mu C$

Correct answer:

$40 \mu C$

Explanation:

Relevant equations:

Q = CV

$\frac{1}{C_{eq, series}} = \frac{1}{C_1} + \frac{1}{C_2}$

First, find the equivalent capacitance of the whole circuit:

$\frac{1}{C_{eq,series}}= \frac{1}{5} + \frac{1}{10} = \frac{3}{10}$

$C_{eq, series} = \frac{10}{3} \mu F$

Use this equivalent capacitance to find the total charge:

$Q = CV = (\frac{10}{3} \mu F) * (12 V) = 40 \mu C$

Capacitors in series always have the same charge on each unit, so the charge on the $5 \mu F$ capacitor is also $40 \mu C$ .

Report an Error

Example Question #1 : Resistors

Resistors are one of the most important basic components of a circuit. With very few exceptions, all circuits have at least one kind of resistor component. An ammeter is a device that measures current flowing through a circuit. Ammeters are always connected to a circuit in series.

Which of the following accurately explains why ammeters must be connected in series within a circuit, and never in parallel?

Possible Answers:

An ammeter connected in parallel would give readings of half the current flowing through the circuit because current would flow evenly between the ammeter and the circuit's regular pathway

An ammeter connected in parallel would give high readings of current because the current would be flowing through both the regular current path and the ammeter, but disproportionately through the ammeter

An ammeter connected in parallel would give the current flowing through the circuit a pathway with minimal resistance, creating a very large current that could harm the ammeter

An ammeter connected in parallel would give very low readings of current because current would be flowing through both the regular current path and the ammeter, but disproportionately through the regular path

An ammeter connected in parallel would not read any current because the current would have no driving force through the ammeter

Correct answer:

An ammeter connected in parallel would give the current flowing through the circuit a pathway with minimal resistance, creating a very large current that could harm the ammeter

Explanation:

In order to give accurate readings of current, ammeters have very low resistances. If connected in parallel, the voltage pushing current through the circuit would push a very strong current through the ammeter and virtually no current through the circuit's regular path. This would not only lead to a bad reading of current, but more often than not a broken ammeter. This phenomenon is an indication of why resistors are so important: they limit the current such that a circuit does not exceed its current-carrying capacity.

Report an Error

Example Question #211 : Ap Physics C

A battery is measured to have a potential of 5V. When connected to a wire with no resistors or other components, the voltage measured is 4.9V.

Why was the potential of the battery measured differently when the wire was connected?

Possible Answers:

The wire is causing electrons to be lost to the air, which lowers the potential measured

The difference in potential measured is small enough to be disregarded

The wire connected to the battery must be connected to something else where this potential is being lost

Once the current is distributed across the wire, there is less charge per unit length of the circuit and so the voltage is lower

The wire has a slight internal resistance and caused a potential drop

Correct answer:

The wire has a slight internal resistance and caused a potential drop

Explanation:

All wires have at least some internal resistance. The most likely explanation for this is that the wire is displaying slight resistance, and therefore caused the measured potential to be less than it was before.

Report an Error

Example Question #3 : Resistors

Three resistors and a battery form the following circuit.

Circuit_1

Calculate the equivalent resistance if the resistors have the following values.

$R_1=40\Omega$

$R_2=25\Omega$

$R_3=38\Omega$

Possible Answers:

$R_{123}=2.5\Omega$

$R_{123}=134.5\Omega$

$R_{123}=92.3\Omega$

$R_{123}=45.2\Omega$

$R_{123}=24.5\Omega$

Correct answer:

$R_{123}=24.5\Omega$

Explanation:

First, calculate the equivalent resistance of R_2 and R_3 . Since these two resistors are arranged in series, we just take the sum of their values.

$R_{23}=R_{2}+R_{3}$

$R_{23}=25\Omega+38\Omega$

$R_{23}=63\Omega$

With resistors 2 and 3 combined together in a single value, the following circuit is formed.

Circuit_2

Notice that and $R_{23}$ are arranged in parallel. To calculate the equivalent resistance of this parallel pair, we use the following equation.

$\frac{1}{R_{123}}=\frac{1}{R_1}+\frac{1}{R_{23}}$

Plug in the values, and solve for 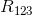$R_{123}$ .

$\frac{1}{R_{123}}=\frac{1}{40\Omega}+\frac{1}{63\Omega}$

$R_{123}=24.5\Omega$

This is just like the circuit shown below.

Circuit_3

Report an Error

Example Question #1 : Current

A lamp has a 60W bulb. If the house wiring provides 110V to light up that bulb, how much current does the bulb draw?

Possible Answers:

$0.72\ \text{A}$

$0.55\ \text{A}$

$1.37\ \text{A}$

$5.83\ \text{A}$

$0.03\ \text{A}$

Correct answer:

$0.55\ \text{A}$

Explanation:

The formula for power is , P=IV and we are given the following values.

$P=60\ \text{W}$

$V=110\ \text{V}$

Solve for the current, .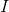

$I=\frac{P}{V}=\frac{60\ \text{W}}{110\ \text{V}}=0.55\ \text{A}$

Report an Error

View Tutors

Om
Certified Tutor

Pune University India, Bachelor of Science, Physics. CUNY Graduate School and University Center, Doctor of Philosophy, Nuclea...

View Tutors

Garth
Certified Tutor

View Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

All AP Physics C Electricity Resources

1 Diagnostic Test 46 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Denver, GMAT Tutors in Chicago, ISEE Tutors in San Francisco-Bay Area, SAT Tutors in San Francisco-Bay Area, Reading Tutors in Boston, ISEE Tutors in Phoenix, Spanish Tutors in Washington DC, GRE Tutors in Washington DC, LSAT Tutors in Seattle, Spanish Tutors in Boston

Popular Courses & Classes

Spanish Courses & Classes in New York City, GMAT Courses & Classes in Denver, LSAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Atlanta, Spanish Courses & Classes in Denver, LSAT Courses & Classes in Miami, ISEE Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Denver

Popular Test Prep

SSAT Test Prep in Phoenix, ISEE Test Prep in San Francisco-Bay Area, GMAT Test Prep in San Diego, LSAT Test Prep in Seattle, SSAT Test Prep in Houston, GMAT Test Prep in Miami, GMAT Test Prep in Denver, LSAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Boston, MCAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Physics C Electricity : AP Physics C

Study concepts, example questions & explanations for AP Physics C Electricity

All AP Physics C Electricity Resources

Example Questions

Example Question #1 : Electric Circuits

Example Question #2 : Electric Circuits

Example Question #3 : Capacitors

Example Question #4 : Capacitors

Example Question #4 : Capacitors

Example Question #3 : Electric Circuits

Example Question #1 : Resistors

Example Question #211 : Ap Physics C

Example Question #3 : Resistors

Example Question #1 : Current

All AP Physics C Electricity Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: