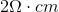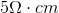All AP Physics 2 Resources
Example Questions
Example Question #1 : Understanding Dc Circuit Diagrams

In the circuit above, what is value of 


The first step to solving this problem is to try to simplify it. We can combine resistors 

Now, we have a single loop with multiple circuit components all connected in series. To calculate the current going through this loop, we need to use Kirchoff's loop law, which says that the sum of all the voltages in a single loop is equal to 0.
This may look confusing at first. Starting from the bottom left point in the circuit, let's begin to go around the loop. The voltage on the battery is +12. The voltage of the resistor is 

Continuing on to the capacitor, the voltage across it is 
Finally, on to the equivalent resistor, the voltage across it is 
Plugging in all the numbers from the problem and solving the equation above for 
Example Question #2 : Understanding Dc Circuit Diagrams
Calculate the value of 
Our first step in solving this circuit is to find the equivalent resistance of 

This is the same as the following equation, which may look more familiar; however, the first equation only works for two elements.
Now that we have the equivalent of the two resistances, we can combine it in series with 

Now that we have the total resistance, we can combine it with the total voltage given in the problem and use Ohm's law to calculate the current.
Example Question #3 : Understanding Dc Circuit Diagrams

Given that 






The key to solving this problem is to recognize the structure of the circuit. The voltage source, the capacitor, and the two resistors are in parallel to each other, meaning that they have the same voltage! This is a very important concept and will make many problems easier to solve.
Since the branch containing the two resistors has 5V, we can easily solve for the voltage of 
One easy way to solve for the voltage is to calculate the current going through the entire branch. Keep in mind here that two resistors in series have the same current.
Now that we have the current that flows through each of the two resistors, we can calculate the voltage drop across only the first resistor.
Example Question #41 : Circuit Properties

In the circuit diagram above, what do each of the letters represent?
A: Battery
B: Resistor
C: Solenoid
D: Capacitor
A: Capacitor
B: Solenoid
C: Resistor
D: Battery
A: Resistor
B: Battery
C: Solenoid
D: Capacitor
A: Battery
B: Solenoid
C: Capacitor
D: Resistor
A: Battery
B: Resistor
C: Capacitor
D: Solenoid
A: Battery
B: Resistor
C: Capacitor
D: Solenoid
A represents a battery. Convention dictates that the direction of charge flow is from the small side to the large side. B is a resistor. Its symbol makes sense if you view the flow of electrons similarly to water flowing; water's flow is resisted by turns, so the jagged lines would evoke that thought for electrons flowing. C is a capacitor. Common capacitors are parallel plates of equal surface area separated by a vacuum or dielectric. This is why the lines are equal in length, unlike the battery. D is a solenoid. A solenoid is a coil of wire that induces a magnetic inside of it.
Example Question #41 : Circuits

If 


The time constant of this RC circuit is only dependent on the value of the resistance and the capacitor, not the voltage source.
Example Question #1 : Resistivity
You have a 4cm long copper wire with a radius of 0.5mm. You have experimentally determined the resistance of the wire to be 
None of the other answers is correct
The resistivity of a material is how much the material resists the flow of charge through it. Metals have low resistivities (which makes them good conductors), while things like glass or plastic have high resistivities.
The equation for resistivity is as follows:








We're given the radius of the wire, so to find the area, we square the radius and multiply it by 
Now, we can plug in our values.
Therefore, the answer is 
Example Question #1 : Resistivity
You create a cylinder of an unknown material that has a diameter of 


What is the resistivity of the material?
Use the equation for resistivity:
First, find the cross sectional area.
Plug in known values.

Example Question #2 : Resistivity
You have a sample that is a cube of volume 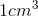

What is the resistivity of the material?
Since we have a cube of volume 

Rearrange the equation and plug in known values.
Example Question #3 : Resistivity
You have a material with resistivity 


What will be the resistance of this component?
None of these
Use the resistivity equation:
Example Question #5 : Resistivity
You are researching new materials for usage in spacecraft electronics.
You have a new material, known as "Type F."
You carve out a cylinder of the material. It is 

You put electrodes on each face of the cylinder.
You determine the resistance to be 
What is the resistivity of "Type F?"
None of these
We will use the relationship
Where 



Remember that the area of a circle is
Combining our equations we get
We then need to plug in our values
All AP Physics 2 Resources