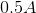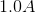All AP Physics 2 Resources
Example Questions
Example Question #21 : Circuits
A single 

Use Ohm's law:
Converting 
Example Question #21 : Circuits
In the circuit above, find the current through 
None of these
First, find the total resistance of the circuit.


Next, add the series resistors together.
Use Ohm's law to find the current in the system.
The current through 


Also, the voltage drop across them need to be equal, since they are in parallel.
Set up a system of equations.
Solve.
Example Question #21 : Circuit Properties
In the circuit diagram shown below, both resistors have a resistance of 



The current will increase by a factor of
The current will not change
The current will halve
The current will double
The current will decrease by a factor of
The current will not change
In this question, we're shown a circuit diagram with two resistors connected in parallel. We're also told that both resistors have the same resistance. We're then asked to determine how the current through one of the resistors will change if the other one is removed.
To answer this question, we'll need to take Ohm's law into account, which states the following.
Moreover, for two resistors connected in parallel, the equivalent resistance is found by summing the inverses of the individual resistors. In the event that two resistors have the same value, as in this case, the equivalent resistance will be cut in half.
Since the equivalent resistance of the circuit is half as great as either resistor, the removal of 
Now, it's important to realize that the current of the entire circuit becomes half as great. But remember that in the original circuit, the overall current (which was twice as great) was split between the two resistors. Thus, even though the overall current in the circuit is being cut in half, the entirety of the new current is flowing solely through 
Example Question #191 : Electricity And Magnetism
You have a circuit with a 

To find the current in a circuit with a battery and resistor(s), you use Ohm's Law.
We have the voltage and we have the resistance, so we don't need to rearrange the equation.
Therefore, the current through the resistor is 2 amps (
Example Question #1 : Current And Voltage
A 

There's not enough information to determine the resistance of the wire
The relevant equation for this problem is Ohm's law.
We're given the voltage and the current, so we need to rearrange to get the resistance.
Example Question #2 : Current And Voltage
Consider a circuit connected to a 

To begin with, we'll need to calculate the current that is flowing through this circuit. We can do this by using Ohm's law.
Now that we have an expression that gives us the current, which is in units of charge per second, we'll need to calculate the moles of charge per second.
This expression directly above gives the total amount of charge that passes within a given time frame. But to find the moles of charge, we'll need to use Faraday's constant.
Example Question #1 : Current And Voltage

Determine the current through 
First, we need to find the total resistance of the circuit. In order to find the total resistance of the circuit, we need to combine all of the parallel resistors first, then add them together as resistors in series.
Combine 

Combine 

Combine 

Then, add the combined resistors, which are now all in series:

Then, we will need to use Ohms law to determine the total current of the circuit
Combine all of our voltage sources:
Plug in our values:
We know that the voltage drop across parallel resistors must be the same, so:
Use Ohm's law:
We also know that:
Substitute:
Solve for 
Example Question #23 : Circuit Properties

Determine the current through 
First, we need to find the total resistance of the circuit. In order to find the total resistance of the circuit, we need to combine all of the parallel resistors first, then add them together as resistors in series.
Combine 

Combine 

Combine 

Then, add the combined resistors, which are now all in series:
Then, we will need to use Ohm's law to determine the total current of the circuit:
Combine all of our voltage sources:
Plug in our values:
We know that the voltage drop across parallel resistors must be the same, so:
Use Ohm's law:
We also know that:
Substitute:
Solving for 
We plug in our values:
Example Question #29 : Circuits

Determine the current through 
First, we need to find the total resistance of the circuit. In order to find the total resistance of the circuit, we need to combine all of the parallel resistors first, then add them together as resistors in series.
Combine 

Combine 

Combine 

Then, add the combined resistors, which are now all in series:
Then, we will need to use Ohms law to determine the total current of the circuit.

Combine all of our voltage sources:
Plug in our values:
We know that the voltage drop across parallel resistors must be the same, so:
Use Ohm's law:
We also know that:
Substitute:
Solve for 
Plug in our values:
Example Question #30 : Circuits

Determine the current through 
First, we need to find the total resistance of the circuit. In order to find the total resistance of the circuit, we need to combine all of the parallel resistors first, then add them together as resistors in series.
Combine 

Combine 

Combine 

Then, add the combined resistors, which are now all in series:
Then, we will need to use Ohm's law to determine the total current of the circuit.
Combine all of our voltage sources:
Plugin our values:
We know that the voltage drop across parallel resistors must be the same, so:
Use Ohm's law:
We also know that:
Substitute:
Solving for 
Plug in our values:
All AP Physics 2 Resources