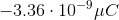Using Gauss's law:

Where is the electric field at the surface of the enclosed shape

is the surface area of the shape

is the charge enclosed

is

Solving for

Surface area of a sphere:

Plugging in values:

 is considered the flux.

Plugging in values:

We need the charge enclosed by a gaussian surface (in this case, we'll use a sphere because there's spherical symmetry) to be zero. When this happens, there cannot be any electric field as 

All the charge is uniformly distributed, so the charge density of the inner sphere is  and on the outer sphere is . We only need to use the outer sphere's surface density since the zero electric field point cannot enclose zero charge in the inner sphere since it's only enclosing negative charge. 

The distance where there is no electric field will be when the gaussian surface encloses  from the outer sphere in order to cancel the  from the inner sphere.

Because everything is uniformly distributed:

.  is charge,  is charge density, and  is volume. We need this to equal 

This is the volume of just the outer surface needed. To find the distance, we just use the formula for the volume of a thick spherical shell and algebra.

Let  be the distance where there will be zero electric field.

This gives 

Because we're talking about electrons, the answer must be negative. The way to solve this is to find how many electrons are in 1.5 kg of water. First, we need to convert kilograms of water into grams of water:

Then, we can use the provided molar mass of water to calculate the number of moles of water in 1.5kg of water:

Once we know how many moles of water we have, we can use Avogadro's number () to calculate how many molecules of water are in 83.33mol.

Once we know how many molecules of water we have, we can multiply by 10 to figure out how many electrons those molecules represent, since we are told that each water molecule has 10 electrons.

Finally, we can multiply by the provided charge of an electron to calculate the charge of those electrons.

The elemental charge is the magnitude of charge, in Coulombs, that each electron or proton has. Because electrons have a negative charge, don't forget to add a negative sign into the equation.

When you convert the answer to microcoulombs, the answer is :

The equation for the quantity of charge is:

where  is the charge quantity,  represents the number of electrons, and  is the charge of an electron, also known as the elementary charge.

Rewrite the equation.

One coulomb, , consists of electrons,

Substitute these two values into the formula.

This number represents the electron's fundamental charge. 

Because this is a neutral balloon, the net charge is equal to the charge the was removed, but opposite in sign. There were 16,000 electrons removed, each of which has a charge of . Therefore, the total charge that was                       removed is:

To answer the question, we must remember that if that much charge was removed from the balloon, the balloon will now be negative.

Surface area of sphere:

Plug in values:

A way to think of flux is to count the number of electric field lines exiting a shape and subtract from it the number of field lines entering the shape. The only way for there to be more lines exiting the shape than entering the shape (and the only way to have any flux) is when the shape is enclosing charge.

In our problem, the box has no charge in it. Therefore, it has the same amount of field lines leaving it as it does entering it. This means that there is 0 net flux through the box. 

Because the box is a conductor, the electrons are able to shift when charge is applied. Because the box is isolated, there is nothing else exerting influence over the box.

The electrons on the shell are able to move from the electric field made by , so they group together on the inner surface of the box to make a net charge of . Because  worth of electrons moved from the outer surface, the outer surface necessarily has a net charge of  now, because it was neutral before.