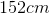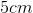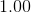Parallel rays that reflect off a concave mirror always pass through the focal point of the mirror. 

In this question, we're told that an object is positioned outside of the curvature radius of a concave mirror. We're asked to identify how the resulting image will appear.

One way to approach this problem is to draw a ray diagram. In such a diagram, a straight line is first drawn from the top of the object horizontally to the mirror. From there, the line is drawn to pass through the mirror's focal point.

A second line is then drawn from the top of the object and straight through the focal point to the mirror. Then, the line is drawn horizontally away from the mirror.

The point at which these two lines intersect will represent the top of the image. In the diagram shown below, we can see that the image will appear in front of the mirror. Hence, it is a real image. Furthermore, the image appears upside down, meaning that it has an inverted orientation. So all together, the image will be real and inverted, which makes this the correct answer.

A telescope with an objective lens with a diameter  with a wavelength of light  can barely resolve two objects with an angular separation of  using

The separation distance between the two objects, we will call this , and the distance to the objects from the telescope objective  can be related to the tangent of that angle,

You are far away from the lights and this angle is very small so the small angle approximation can be used,

Setting these expressions for  equal and solving for  and converting from  to ,

In this question, we're presented with a scenario in which an object is placed a certain distance in front of a thin convex lens. After being given the radius of curvature for this lens, we're asked to determine certain properties of the image; whether it will be real or virtual and whether it will be up-right or upside down.

To begin with, let's use the following equation:

Where  is equal to the distance of the object from the lens

 is equal to the distance of the image from the lens, and

 is equal to the focal length of the lens

In order to calculate the focal length, we'll need to use the radius of curvature. The focal length is simply half this value:

Now that we have the focal length, we can calculate the image distance by first isolating the term:

Next, we can plug in values to obtain the image distance:

The value that we have obtained for the image distance is negative. This means that the image formed in this scenario will be a virtual image.

Moving forward, we can use the image distance and object distance in order to determine the orientation of the image (the magnification):

Since the value we obtained is positive, we can conclude that the image will be formed up-right.

In order to solve this problem, we first must find where the image is located, and then we can use that to find the image's height.

The formula needed is:

-focal length

-distance man is from lens

-distance image is from lens (positive is on the other side of the lens with respect to the man)

In this case we have

We get 

Now we can use the formula 

-image height

-object height

to find the height of the image.

This means the image height is , or  inverted.

One of the rules of drawing ray diagrams is that if the ray goes through the focal point on one side and hits a thin lens, then the ray will emerge parallel to the principal axis. 

This question is asking us to determine the properties of the image formed by a converging lens when the object is located at a distance that is beyond the focal point of the lens.

One way to go about solving this problem is to draw a visual diagram showing ray vectors, as shown below.

In the above diagram, we have an object located on a flat surface, along with a converging lens to the right of it and the focal points on either side of the lens. After drawing these in, we need to draw our light rays as coming from the top of the object, and we'll need to use a total of three lines.

The first line is drawn horizontally from the top of the object to the middle of the lens. From there, this line is drawn passing through the focal point on the right.

The second line drawn is on the bottom in the picture above. This line is drawn from the top of the object and through the left focal point until it reaches the middle of the lens. From there, the ray is drawn from the middle of the mirror and straight horizontally.

Finally, the third line is drawn from the top of the object and through the very center of the lens.

At the point where all three of these lines intersect is where we will find the top of the image. As can be seen above, the top of the image will be facing downwards, and is therefore inverted.

To determine if the image is real or virtual, we have to ask ourselves: Are the light rays going where they're supposed to go, or did we have to extrapolate the rays to find our image? In this case, the rays went where they are supposed to go, which is through the lens and to the opposite side. Therefore, the image formed is real.

This problem can be solved using Snell's law:

Rearrange to solve for for the index of refraction of water

We can determine the second angle:

We have all the values for Snell's law, allowing us to solve:

To find the index of refraction, we use Snell's Law:

We have values for _, , and , so now we just need to rearrange the equation to solve for .

Now, we can just plug in our numbers.

Therefore, the index of refraction of the second material is 1.346.

To find the angle of refraction, use the Snell's law equation to determine the angle.

Find the index of refraction for water.

Find the index of refraction for air.

Solve for .