All AP Physics 2 Resources
Example Questions
Example Question #1 : Wavelength, Frequency, And Period
What is the wavelength of a sound traveling at a frequency of 3000Hz?
The wavelength of a sound can be found by utilizing the equation, 

Example Question #141 : Ap Physics 2
At a local concert, a speaker is set up to produce low-pitched base sounds with a frequency range of 20Hz to 200Hz, which can be modeled as sine waves. In a simplified model, the sound waves the speaker produces can be modeled as a cylindrical pipe with one end closed that travel through the air at a velocity of 
How are the first three harmonics of the base speaker designated?
1, 3, 4
1, 2, 3
1, 3, 5
1, 2, 5
1, 3, 5
First, notice that the paragraph above tells us that the wave can be modeled as a pipe with one end closed. This is in contrast to the other possibility, where the wave is modeled as a pipe with two ends open. It is critical to recognize this difference, as the definition of sequential harmonics and the formula used to calculate them changes depending on whether both ends are open or not. In the situation where one end is closed, the harmonics are odd numbers, meaning that the first three harmonics are 1st, 3rd, and 5th. In the situation where both ends are open or both ends are closed, the harmonics are sequential, meaning that the first three harmonics are 1st, 2nd, and 3rd.
Example Question #181 : Mcat Physical Sciences
At a local concert, a speaker is set up to produce low-pitched base sounds with a frequency range of 20Hz to 200Hz, which can be modeled as sine waves. In a simplified model, the sound waves the speaker produces can be modeled as a cylindrical pipe with one end closed that travel through the air at a velocity of 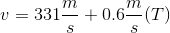
How long would it take for a 30Hz beat to reach an audience member 100m away when the ambient temperature is 21ºC?
0.91s
0.31s
0.11s
0.29s
0.29s
The question asks us to determine how long it will take for a wave beat to reach an audience member at 100m away; thus, we need to calculate the velocity of the wave to determine the time.
We know from kinematics that 

Example Question #19 : Waves
At a local concert, a speaker is set up to produce low-pitched base sounds with a frequency range of 20Hz to 200Hz, which can be modeled as sine waves. In a simplified model, the sound waves the speaker produces can be modeled as a cylindrical pipe with one end closed that travel through the air at a velocity of 
What is the closest distance a person could be standing away from the speaker in order to hear the loudest fundamental frequency of a 1.2m wavelength wave at the concert?
1.1m
0.3m
1.9m
0.7m
0.3m
This question asks us to incorporate information we learned in the pre-question text and new information in the question. First, we are told that we are looking to calculate a distance where maximal sound is heard, in other words, where the amplitude is at its maximum. This only occurs at an anti-node.
Additionally, we know that the speaker can be modeled as a one-end closed pipe, meaning that the wavelengths of the harmonics are calculated as 
In a one-end closed pipe model, each harmonic ends with maximal amplitude, so we can find L (the length of the pipe, i.e. where the person standing would hear maximal sound), as we know the fundamental harmonic has n = 1.
Example Question #3 : Intensity And Decibels
At a local concert, a speaker is set up to produce low-pitched base sounds with a frequency range of 20Hz to 200Hz, which can be modeled as sine waves. In a simplified model, the sound waves the speaker produces can be modeled as a cylindrical pipe with one end closed that travel through the air at a velocity of 
Find the intensity of a 35dB base wave produced by the speaker.
This question asks us to determine the intensity of a wave, given to us as a comparison of the wave intensity to the intensity of the limit of human hearing. In math terms, we know that the decibel scale is calculated as shown below.
I0 is the limit of human hearing (10-12 W/m2).
Example Question #2 : Harmonics And Standing Waves
Which of the following is a standing wave?
A bus rumbling over a metal bridge
The sound made by an electric fan
Light with a wavelength of exactly
Ocean waves hitting a pier every ten seconds
A vibrating violin string
A vibrating violin string
A simple definition of a standing wave is a wave that is self-reinforcing, which is to say that reflection of the wave through the medium results in some areas of amplification (anti-nodes) of the wave and some areas of nullification (nodes). In other words, resonance must occur, and that usually suggests confinement of the wave in some fashion.
A fan and a bus make noise and vibration, but the sound does not resonate. It is transmitted, but not confined. Light with a specific wavelength has no "resonant" character, and neither do waves striking a pier. If the waves were confined in a harbor so that they could amplify, it might be possible to produce a standing wave. Microwaves trapped inside a microwave oven have this feature, producing antinodes of intense heating and nodes where no energy is transmitted into the food; this is the reason that microwave ovens have rotating platforms to make heating of the food item more uniform.
A violin string will be seen to have discrete, stable regions of motion and lack of motion, the requirements of the standing wave phenomenon. The points of reflection on the string are the two ends. The vibration of the wave is confined within the string, amplifying the sound as the nodes overlap.
Example Question #3 : Harmonics
If the first overtone of a sound wave in a pipe with one end open and one end closed has a frequency of 300Hz, what is the frequency of the second overtone?
In an open-closed pipe, we get only odd harmonics, since there must always be a displacement node at the closed end and a displacement antinode at the open end. So, the first overtone is the same as the third harmonic, which has 




Example Question #4 : Light
A red light (wavelength = 6.5 * 10-7m) shines on a diffraction grating, creating an interference pattern on a distant screen. If a blue light (wavelength= 4.75 * 10-7m) were shone on the same screen instead, the bright lines on the screen would __________.
move farther apart
move closer together
become brighter
remain the same
become dimmer
move closer together
The bright lines from a diffraction grating can be located with the equation 





Example Question #21 : Waves
Each of the following types of waves experience polarization except __________.
transverse waves
light waves
sound waves
electromagnetic waves
sound waves
Polarization is the property that allows tansverse waves to oscillate in multiple orientations. A transverse wave can oscillate, for example, in either the xy-plane or the yz-plane.
Sound waves are longitudinal, and thus do no experience polarization as medium is displaced in one direction only. A longitudinal wave will travel in only one dimension via compression and rarefraction.
Example Question #191 : Mcat Physical Sciences
A light ray traveling through a medium is reflected by a second medium at an angle of 20⁰ to the interface between the two media. Which of the following is true?
The refractive index of the second medium is equal to sin(20⁰)
The refractive indices of the media must be equal
The frequency of the light wave is greater upon reflection
The angle of reflection is 70o
The angle of reflection is 70o
The angle of reflection is the angle between the reflected light ray and a line perpendicular to the interface between the two media. The angle of reflection must be complementary to 20o.
90o – 20o = 70⁰
All AP Physics 2 Resources





























