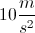Using the equation for momentum,

If the mass stays constant and the velocity doubles, the momentum must double as well to balance the equation.

Because we are solving for two velocities (two unknowns), we need two equations. We can use the conservation of linear momentum:

Because we know that the collision is elastic, we know that kinetic energy is conserved:

The red ball starts at rest so

The above equations can then be simplified and one can solve for and .

Negative implies the ball is moving to the left.

Using conservation of momentum

Solving for 

Plugging in values:

(A negative value is assumed for Tommy's direction for simplicity, a negative could have been used for Jennifer's instead, it will yield the same result.

A coordinate system isn't immediately given, so the first step is to establish an x- and y-direction. Let the first ship travel in the positive y-direction with the second traveling  from the y-axis.

The linear momentum for the first ship is given by 

and for the second ship by 

Conservation of linear momentum says that . Thus the final velocity can be expressed as

Further,

The final speed is then 

This question tests your understanding of the concept of conservation of momentum. More specifically, this tests your understanding of perfectly inelastic collisions, or collisions in which the two colliding particles stick together and move together as a system. 

By conservation of momentum, the initial total momentum of a system is equal to the final total momentum of the system. The formula for the momentum of an object is equal to the mass of the object multiplied by the velocity of the object. When applying the conservation of momentum formula to perfectly inelastic collisions, you consider the two objects as a single mass after they collide, since they stick together and travel together. Thus, this problem can be solved as follows:

The final velocity of the  ball unit is therefore (sign is positive because initially the  ball was traveling to the right, and its velocity was positive, and when the  ball unit formed and moved, it continued moving in the rightward, positive direction.

This question tests your understanding of the conservation of momentum, which states that momentum (mass multiplied by velocity) can neither be created nor destroyed in a system. In this elastic collision, we are presented with two blocks (one initially moving, and one initially stationary), that collide such that each block is moving separately afterwards and neither loses energy to friction or other forces. You can set up the equation as follows:

Therefore, the final velocity of the  block is  in the positive direction.

We know that the plane needs to drop 3,000 meters in 10 minutes. Therefore, we can calculate the vertical velocity that the plane needs to be traveling at:

Knowing the plane's velocity, we can caluclate what angle at which it needs to decend to achieve this vertical velocity:

Rearranging for theta:

Plugging in our values:

We can use our kinematics equations to determine the height of the rocket the moment it loses thrust:

If we clarify the initial state being the moment the rocket loses thrust and the final state being the point of its maximum height, we can use the expression for conservation of energy to calculate the final height:

Removing final kinetic energy (which will be zero) and substituting in our expressions for each variable:

Cancel out mass and rearrange for final height:

From the problem statement, we can determine the initial velocity:

Now that we have values for all of our variables, we can solve:

There are two ways to solve this problem. The first and much easier way is to use the range equation. The second is using your kinematics equations.

Method 1: Range Equation

The range equation is the following:

We know everything ecvept for the initial velocity. However, we can calculate it knowing that the cannon transfers 500 J of energy to the ball. Therefore:

Rearranging for velocity:

Now we can plug everything into the range equation:

Method 2: Kinematics Equations

As in the first method, we can calculate the initial velocity of the ball:

Rearranging for velocity:

We can then split this into it's components:

We can use the y-component to calculate how long the ball is in the air. We can do one of two things:

1. Calculate how long the ball takes to reach it's peak and then multiply by 2
2. Calculate how lon gthe ball takes to get a velocity of -5

We'll go with method 2:

Rearranging for t:

Then we can multiply this time by the horizontal velocity (which stays constant because we are neglecting air resistance).

To find the acceleration of the box traveling down the incline, the mass is not needed. Using the incline of the plane as the x-direction, we can see that there is no movement in the y-direction; therefore, we can use Newton's second, F = ma, in the x-direction.

There is only one force in the x-direction (gravity), however gravity is not just equal to “mg” in this case. Since the box is on an incline, the gravitational force will be equal to mgsin(30^o). Substituting force into F  =ma we find that mgsin(30^o) = ma. We can now cancel out masses and solve for acceleration.