All AP Physics 1 Resources
Example Questions
Example Question #272 : Linear Motion And Momentum
Consider the following system:
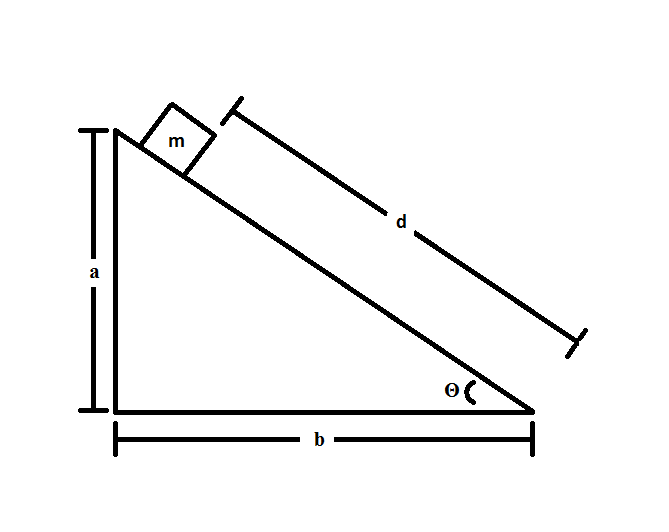
If 

There are two forces in play in this scenario: friction and gravity. We can use Newton's second law to develop an expression for the acceleration of the block:
Substituting in expressions for each force, we get:
Canceling out mass and rearranging for acceleration, we get:
We know all of our values, allowing us to solve for the acceleration:
Example Question #512 : Newtonian Mechanics
A young boy is aiming a slingshot straight upward. If the sling shot applies 

We can use the equation for conservation of energy to solve this problem:
If we assume the initial state is when the slingshot is fully loaded and the final state is at the ball's maxmium height, we can completely eliminate kinetic energy to get:
Substituting in our value for initital potential energy and an expression for final potential energy, we get:
Rearranging for final height we get:
Example Question #513 : Newtonian Mechanics
A sports car can accelerate from 

The basic kinematics equation for motion under constant acceleration is:
We do not have the acceleration, but we can find it:
Apply this to the first equation and solve.
Example Question #514 : Newtonian Mechanics
A walker is walking at a constant rate of 

The equation for speed is:
The runner has gone around the track 1.5 times, thus his total distance traveled is:
We can find the elapsed time from the walker: Rearrange the speed equation to find time:
Now we have all the information we need to find the runner's speed:
Example Question #515 : Newtonian Mechanics
An object is moving to the right and is speeding up. Which of the following is false?
The magnitude of the object's velocity increases
The object experiences a positive net force
The object's acceleration is positive
The object's velocity is positive
The object experiences a net force of 0N
The object experiences a net force of 0N
If an object is moving to the right, then its displacement is positive. If its displacement is positive then its velocity must be positive as well. The object is speeding up. This implies that the magnitude of its velocity is increasing. If this is true we have that the velocity of the object, 



So we have that the object's acceleration is positive. If the object's acceleration is positive, then there must be a positive net force causing the acceleration, due to Newton's first law: 
Example Question #516 : Newtonian Mechanics
Which of the following statements is false regarding the relationship between an object's velocity and acceleration?
If both the object's acceleration and initial velocity vectors are negative, then the object will slow down
If the object's acceleration is positive and its initial-velocity is negative, then the object will slow down
If an object experiences constant velocity, then its acceleration is 0
If an object experiences a nonzero acceleration, then its velocity will change
If both the object's acceleration and initial velocity vectors are positive, then the object will speed up
If both the object's acceleration and initial velocity vectors are negative, then the object will slow down
By definition, acceleration is the rate of change of velocity with respect to time. The average acceleration of an object is given by:
Therefore, if velocity is constant it must be the case that acceleration is 0, since the initial and final velocities of the object are equal. Similarly, if acceleration is non-zero, then it must be the case that the initial and final velocities of the object are different (so velocity is changing). Now, when an object's acceleration and initial-velocity have the same sign (i.e. the same direction) then the object will speed up. In other words, the absolute value of its velocity (the magnitude) increases. This is easy to see if we solve for the final velocity in our equation:
If both 




Example:
Example:
Remember that the positive and negative signs indicate the direction of the vectors. So when it comes to slowing down or speeding up, we want to look at the magnitude of the velocity. Therefore, the only statement that is false is the one that says that if an object has both negative initial velocity and acceleration it will slow down. The object will speed up and continue to move to the left.
Example Question #517 : Newtonian Mechanics
An object slides across the floor moving to the left. After some time it comes to a stop. Which of the following is false?
Throughout its trajectory, the object's velocity is greater or equal to
The object's displacement is negative
The magnitude of the object's velocity is decreasing
Throughout its trajectory, the object's velocity is less than or equal to
The object experiences a positive acceleration
Throughout its trajectory, the object's velocity is greater or equal to
If the object is moving to the left, then its displacement must be negative since its final position will be further to the left in than its initial position. So in an imaginary number line, after some time passes, the object's final position is less than the object's initial position. This can be shown mathematically:

Since the object's displacement is negative, then so is its velocity. This can easily be seen from the equation for average velocity:



The object eventually stops. This means that the magnitude of the object's velocity is decreasing. In other words, the absolute value of the object's velocity is becoming smaller and smaller until it stops. So, for example, if at some moment the object's velocity is 



Thus the acceleration must be positive.
Example Question #551 : Ap Physics 1
Imagine a decending elevator that is increasing it's speed. What is the direction of the acceleration of the elevator?
Left
Down
Up
Right
Down
A trick that I often use is if something is speeding up, the acceleration and velocity point in the same direction. If something is slowing down. the acceleration and velocity point opposite directions. Since the elevator is speeding up, the acceleration must point in the same direction as it's velocity: downwards.
Example Question #552 : Ap Physics 1
A ball is thrown straight up in the air. The ball falls back and is caught at the same location it is thrown from. At what locations does the position(y) equal zero, the velocity(v) equal zero, or the acceleration(a) equal zero? Assume the origin of my single coordinate system is placed at the location the ball is thrown.
y=0 when the ball is thrown and caught, velocity is equal to g and never zero, a=0 at the apex
y=0 when the ball is caught, v=0 at the apex, a is equal to g and never zero
y=0 when the ball is thrown and caught, v=0 at the apex, a is equal to g and never zero
y=0 when the ball is thrown, v=0 at the apex, a=0 at the apex
y=0 when the ball is thrown and caught, v=0 at the apex, a=0 at the apex
y=0 when the ball is thrown and caught, v=0 at the apex, a is equal to g and never zero
The origin is placed at the location the ball is thrown and caught so y=0 when it is thrown and caught. Because the ball only moves in one dimension (up or down), the velocity must drop to zero when it transitions from a upward positive velocity to a downward negative velocity at the apex. The acceleration on the surface of earth is always g for projectiles when neglecting air resistance or other forces.
Example Question #553 : Ap Physics 1
Consider three distance vs. time plots. The first displays a horizontal line at 
I
I and II
II
I, II, and III
III
I and II
The slope of a distance vs. time plot represents the object's velocity. Therefore, in both the first and second graphs, the velocity is constant and zero, respectively. An object with constant (or no) velocity is experiencing, by definition, no net force. Oppositely, in the third graph the slope is increasing, meaning the object is accelerating, meaning it must be subject to some force.
Certified Tutor
All AP Physics 1 Resources























































